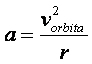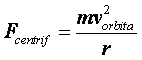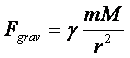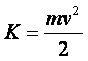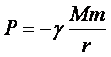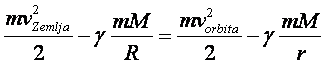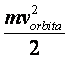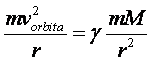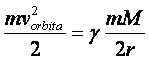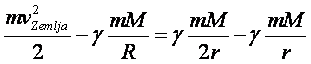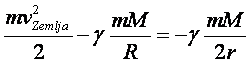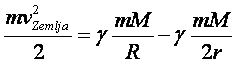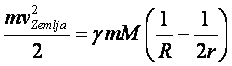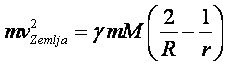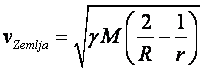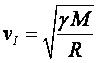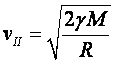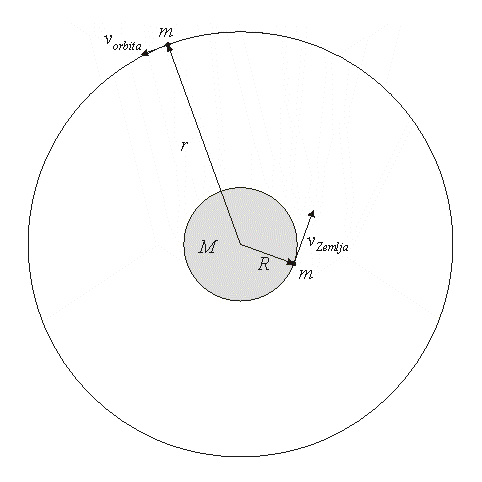
Iz iskustva znamo da kada skočimo uvis, padnemo nazad. Međutim, možemo li skočiti toliko brzo da ne samo što ne padnemo na zemlju, nego još i da se oslobodimo Zemljinog gravitacionog zagrljaja? Koliko brzo bi tada trebalo skočiti? Na ova pitanja pokušaću da odgovorim u ovom tekstu.

Često sam na sajtu »Astronomskog magazina« i u časopisu »Astronomija« nailazio na relativne nedoslednosti oko definicija pojmova »prve«, odnosno »druge kosmičke brzine«. Namera mi je da ovim tekstom »postavim svaku stvar na svoje mesto«, a ujedno ću proširiti taj pojam na bilo koje – dobro, u redu – skoro na bilo koje drugo nebesko telo: prvu i drugu kosmičku brzinu nema samo Zemlja.

Potrebno matematičko predznanje uglavnom obuhvata elementarnu algebru koju bi osnovci trebalo da poznaju, a kada je reč o fizici, đaci prvog razreda gimnazije trebalo bi da poznaju izraze za kinetičku i potencijalnu energiju, zakon održanja energije, centrifugalnu silu i Njutnov zakon gravitacije; međutim, da bi i čitaoci koji ne poznaju dovoljno dobro fiziku mogli da prate ovaj tekst, to sam neophodne definicije ponovio. Dakle, samo hrabro!

S druge strane, verujem da sam i pored priličnog pojednostavljenja problema uspeo da zadržim dovoljan nivo matematičke »strogosti« u dokazivanju, odnosno izvođenju jednačina.

Šta je poznato, a šta ne?

»Početni podaci« koji su nam na raspolaganju su dve brzine, dve mase i dva poluprečnika. (Istina, ne moramo znati svaki od ovih podataka: neke će se već veličine »skratiti«.)

Rešimo problem u »najopštijoj formi«: ono što treba da nađemo je koliku brzinu – označićemo je sa  – treba dati raketi da bi ona zauzela kružnu orbitu oko Zemlje; brzinu koju će raketa dostići u stabilnoj orbiti oko Zemlje označićemo sa . Masu Zemlje oznaćićemo sa , i možemo je naći i na sajtu »Astronomskog magazina«, tako da »to znamo«, a masu rakete označićemo sa  (ta, valjda je masa Zemlje veća od mase rakete!). Konačno, poluprečnici: Zemljin , a poluprečnik orbite  meren je od centra Zemlje. (Očigledno, ali i nebitno za dalju priču, je da je raketa, kada je u orbiti, na visini .)

Sve ove veličine prikazane su na slici.

Očigledno, nam je »u glavnoj ulozi«, odnosno ono što treba da pronađemo: brzinu lansiranja rakete sa Zemlje.

Malo »Njutna« za početak

Kako se raketa vrti oko Zemlje brzinom konstantnog intenziteta, takozvanom linijskom (periferijskom) brzinom, ona će prema tome imati samo normalno ubrzanje. Drugim rečima, intenzitet od  se ne menja. Međutim, da li se sam vektor  menja? O, da! E, mera promene orbitalne brzine (kao vektora!) je čuveno normalno ubrzanje, zaduženo samo i jedino za to da tera raketu da se vrti oko Zemlje. Iz fizike znamo da se ovo ubrzanje računa kao

    (1.1)

Ovo ubrzanje značajno je jer daje centrifugalnu silu, čiji je intenzitet (ne moramo se baš nonstop petljati vektorima...):

    (1.2)

Međutim, prema Njutnovom zakonu gravitacije, Zemlja i raketa uzajamno se privlače! Kakav užas! I koliko samo neophodan užas! (Koliko je neophodan videćete uskoro.) Za sada, zadržimo se na jačini gravitacione sile:

   (1.3)

Ova jednačina predstavlja Njutnov zakon gravitacije, a ljubitelji fizike primetiće da upadljivo podseća na Kulonov zakon. (Ovde je gravitaciona konstanta, koja nam je poznata: ) Pošto nam je raketa u stabilnoj orbiti, nonstop na istoj visini iznad Planete, to znači da su gravitaciona i centrifugalna sila po intenzitetu jednake (mada su, priznajem, suprotnog smera): jedna vuče na jednu stranu, druga vuče na suprotnu stranu, pa se »kompenzuju«. Ali to nam znači da možemo napisati tu strašnu jednačinu (1.4):

  (1.4)

Videćete kasnije koliko je to važna jednačina. Do tada – »stay tuned«...

Šta je sa energijama?

Za energiju (odnosno, preciznije – za energije u mehanici) zna se da važi zakon održanja: ne možeš je niti stvoriti, niti uništiti; ali joj možeš promeniti oblik postojanja. U našem slučaju (sistem Zemlja-raketa) dva su ključna – i jedina interesantna – oblika energije: kinetička i potencijalna. U svakom trenutku zbir kinetičke i potencijalne energije mora biti isti, pri čemu se te dve energije menjaju: koliko jedna poraste, toliko druga opadne, da bi njihov zbir bio nepromenljiv.

Kinetičku energiju obeležiću sa  i računaću je po formuli

, (1.5)

a potencijalnu označiću sa  i računaću je po formuli

  (1.6)

(uočimo znak »minus« u prethodnoj formuli).

Zakon održanja energije tvrdi da je u svakom trenutku kretanja rakete ispunjen uslov:

  (1.7)

Ako je to tako, onda to mora da važi i u dva specijalna slučaja: kada je raketa na površini Zemlje i čeka da bude lansirana, i kada je zauzela stabilnu orbitu oko Zemlje. Koristeći očekivane oznake, napisaću sledeću važnu jednačinu:

 (1.8)

Mora li čovek da bude genije da bi u prethodnoj jednačini prepoznao zakon održanja energije, pomenut na početku odeljka? Naravno da ne!

Uposlimo matematiku!

Scena je postavljena, znamo ko su glavni glumci i predstava može početi! Sada nam je potrebna matematika, kao »alat za zanat«. U jednačinu   (1.8) – zakon održanja energije – menjamo redom jedinačine (1.5) i (1.6) – izraze za kinetičku i potencijalnu energiju, koristeći svaku dvaput: jednom za »situaciju« na površini Zemlje, drugi put za situaciju u orbiti. Tu nema mnogo priče, samo ima da se puno piše. Dakle:

   (1.9)

Ovde su nam sve veličine poznate: mada jesu definisane ranije, jasne su i intuitivno. (Ako se baš ne možeš snaći, pogledaj sliku. U stvari, sliku pogledaj i ako se možeš snaći, da ne ispadne da sam je uzalud crtao.) Priznajem da ovde postoji blaga nedoslednost: velikim sam označio poluprečnik Zemlje, a malim  poluprečnik putanje, premda je očigledno da je  (hej, projektujemo raketu, ne podmornicu!).

Posmatrajmo jednačinu (1.9). Veoma je bitan prvi član na desnoj strani ovog izraza, i ja ću ga za vas ponovo napisati, samo njega:

   (1.10)

Ovde se pojavljuje nepoznata i samim tim i nepoželjna brzina rakete u orbiti oko Zemlje, , i nju nekako moramo izbeći. Sada ćemo se uveriti u moć jednačine (1.4), i njene »mame« i »tate«, jednačina (1.2) i  (1.3)! Iz ovih jednačina – odnosno, iz jednakosti gravitacije i centrifugalne sile – sledi neposredno:

  (1.11)

Ako uporedimo izraz  (1.10) i levu stranu jednačine (1.11) vidimo da upadljivo nalikuju: razlikuju se samo po tome što se u imeniocu prvog izraza nalazi dvojka, a kod drugog je na istom mestu poluprečnik . Pazite sada trik: jednačinu (1.11) pomnožiću nenultom vrednošću , i, kao nekim čudom, dobiću

  (1.12)

Kao što vidite, izraz  (1.10) možemo vrlo lepo zameniti izrazom (1.12): time smo izbegli da koristimo nepoznatu orbitalnu brzinu. Uraaa!

Konačno, možemo koristeći prethodnu jednakost napisati našu jednačinu  (1.9):

   (1.13)

Eto, dobili smo jednu jednačinu sa jednom jedinom nepoznatom veličinom, . Hajde da odredimo tu veličinu. To je u suštini crnački posao, ali – da ga odradimo! (Nagradiću čitaoce jednom anegdotom na kraju poglavlja.) Najpre uprostimo izraz na desnoj strani jednačine: tamo u suštini od jedne polovine »nečega« oduzimamo celo to »nešto«, pa dobijamo negativnu polovinu tog »nečega«:

  (1.14)

(Opet treba povesti računa o znaku »minus«!) Zatim polako radzvojimo nepoznate veličine na jednu stranu, a poznate veličine na drugu stranu:

    (1.15)

Pri kraju smo priče, potreban je još samo mali napor. U desnoj strani gornje jednačine lepo faktorišemo razliku izvlačeći ispred zagrade:

  (1.16)

Pomnoživši gornju jednačinu sa 2, dobićemo

   (1.17)

Nenultu masu  skratimo i neposredno dobijamo jedinstveno rešenje jednačine (1.13):

     (1.18)

Može se reći da je ovde kraj priče. U jednačini  (1.18) sve veličine su nam date, poznate. Ponoviću – ova jednačina nam daje vrednost brzine rakete koju treba da raketa ima da bi stigla u orbitu oko Zemlje, u zavisnosti od mase Zemlje, poluprečnika Zemlje i poluprečnika orbite, bez obzira na to koliki je stvarno poluprečnik orbite. Videćete docnije kako se menjanjem  menja i potrebna početna brzina.

Još da samo proverimo koje smo aproksimacije koristili prilikom izvođenja formule  (1.18). Očigledno je da nigde nismo računali otpor vazduha koji trpi raketa i prilikom lansiranja i tokom stacionarnog stanja. Međutim, taj proračun je previše komplikovan i ja ga ne umem provesti. Mislim da to ne može ni jedan čovek, sam.

Pored toga, pretpostavili smo da je Zemlja, ili bilo koje drugo nebesko telo savršena sfera. Ova priča može se dakle koristiti i za planete, i njihove sferne statelite, i za zvezde (naravno, samo hipotetički, jer za sada nismo u stanju da lansiramo raketu sa površine neke zvezde), ali verovatno neće davati dobre rezultate za nepravilna tela kao što su, recimo, asteroidi: kod njih se uostalom ova brzina menja od tačke do tačke na površi.

Pomenuo sam anegdotu: nakon cele ove matematike, koja, istini za volju, u suštini i nije preteška, mislim da smo zaslužili malo opuštanja. Na beogradskom Elektrotehničkom fakultetu dugo je jedan od profesora matematike bio dr Dobrilo Tošić, inače veoma omiljen među studentima. Priča se da je tokom nekog predavanja profesor na tabli pisao gomilu teških izraza, i kada je došao do tačke od koje je potreban više manuelni nego moždani rad da bi se problem završio, rekao: »E, sada pustimo crnca da sredi ovaj izraz«. Odjednom, iz prepunog amfiteatra iziđe jedan tamnoputi student-stranac, i poče da dovršava taj crnački posao...

Ali – kosmičke brzine...?

Po definiciji, prva kosmička brzina je brzina koju treba saopštiti »telu« (odnosno, raketi) da bi se ona okretala oko Zemlje na maloj visini. Otprilike, kao kada bi Zemlja bila savršena lopta, bez planina i dolina, a mi pustimo raketu na dva metra visine. Šta tada vidimo iz jednačine  (1.18)? U tom slučaju, poluprečnik Zemlje  vrlo je približno jednak poluprečniku putanje rakete , "...pa kada u (1.18) stavimo [R vrlo priblizno jednako r] dobijamo da je ta čuvena prva kosmička brzina:

  (1.19)

Za male visine, a kada je reč o prvoj kosmičkoj brzini visine jesu male, važi relacija , pa kombinujući to sa  (1.19) dobijamo i lako pamtljiv i lako izračunljiv rezultat:

  (1.20)

Koliko je  to zna svako dete, a poluprečnik Zemlje pročitamo npr. »Astronomiji 23« i konačno dobijamo da je ta vrednost vrlo približno

  (1.21)

Po definiciji, druga kosmička brzina je minimalna brzina koju treba saopštiti raketi da bi ona uspela da se iščupa stega gravitacije Zemlje, i ode »beskonačno daleko«, nošena kroz svemir sopstvenom inercijom (odnosno, preciznije – inertnošću). Šta to znači rečeno jezikom matematike? To znači da je rastojanje  vrlo veliko, »beskonačno«. Ako je  stvarno vrlo veliko, onda je recipročna vrednost, , vrlo mala, i u tom slučaju iz jednačine  (1.18) za drugu kosmičku brzinu dobijamo

   (1.22)

Ovde je nezahvalno koristiti činjenicu da je  zbog opadanja ubrzanja Zemljine teže sa visinom, ali kombinujući (1.22) vidimo da drugu kosmičku brzinu možemo predstaviti i kao

  (1.23)

Dakle, druga kosmička brzina veća je od prve kosmičke brzine  puta:

  (1.24)

Ono što je interesantno je da ni prva ni druga kosmička brzina ne zavise od mase rakete koju lansiramo.

***

Šta treba da pamtim?

1. definicije kinetičke i potencijalne energije date jednačinama  (1.5) i  (1.6);
2. jednačine za centrifugalnu silu i gravitacionu silu, date jednačinama  (1.2) i  (1.3);
3. zakon održanja enregije (a i to zna svako dete...);
4. nekoliko trikova u transformacijama jednačina.

Sve ostalo mogu sam da pronađem.

»Za podrobnije upućivanje« (u čast Karlu Seganu):

1. Б.М.Яворский, А.А.Пинский: Основы физики 1
2. Г.С.Ландсберг: Элементарный учебник физики (1. Механика. Теплота. Молекулярная физика.)
3. http://www.astronomija.co.yu/razno/pisma/2004/brzina.htm
4. Božidar Žižić: Kurs opšte fizike – fizička mehanika

Ključne reči

kosmička brzina, prva kosmička brzina, druga kosmička brzina, energija, kinetička energija, potencijalna energija, zakon održanja, zakoni održanja, zakon održanja energije, gravitacija, Njutnov zakon gravitacije

Sažetak

U ovom tekstu definisani su pojmovi prve kosmičke brzine i druge kosmičke brzine. Ponuđen je način za matematičko izvođenje vrednosti ovih brzina. Matematičko-fizički aparat prilagođen je učenicima prvog razreda srednje škole, ali tekst i pored toga mogu pratiti i osobe koje nemaju formalno matematičko ili fizičko predznanje.

Abstract

Terms “circular velocity” and “escape velocity” are defined and explained in this article, with a procedure for mathematical deriving the formulae for both terms. Both mathematical and physical backgrounds used are adapted to junior high-school students, but the paper is still useful to the people who do not have proper math & physics knowledge.

(15.03.2007.)

Komentari

Svaka čast! Potsetili ste me na mog profesora fizike iz drugog razreda Jagodinske gimnazije, zvali smo ga Tomi Stil, i njegovo izvođenje jednačina za prvu i drugu kosmičku brzinu daleke 1963. godine.

Slobodan Maksimović

vrh