|
Idemo redom:
Prva kosmièka brzina
kao što i sam verovatno znaš
predstavlja brzinu potrebnu da bi se neko telo sa Zemlje (ili bilo
kog drugog tela) poslalo u kružnu orbitu,
odnosno postalo satelit (tela sa kog je lansirano, naravno). Naime
ova vrednost se dobija na sledeæi naèin:
da bi telo ostalo u stabilnoj kružnoj
orbiti, gravitaciona i centrifugalna sila moraju da budu uravnotežene.
Znaèi pretoèeno u
matematiku to izgleda ovako:
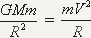 , ,
gde G
predstavlja gravitacionu konstantu, m
masu letelice, M
masu objekta oko koga bi letelica trebala da orbitira (u ovom sluèaju
Zemlje), V
brzinu letelice na toj orbiti, a R
polupreènik orbite u kojoj se letelica
nalazi. Taj polupreènik orbite je zapravo
jednak R = ,
odnosno zbiru polupreènika tela oko koga
satelit orbitira (znaèi ovde Zemlje) i
visine orbite. Tako bi vrednost R za satelit koji se nalazi na 200
km od površine Zemlje bila 6580 km jer
polupreènik Zemlje iznosi 6380 km.
Dalje ako poskraæujemo
ono što se može
skratiti, ostaje:
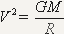 , ,
odakle sledi da je:
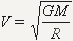 , ,
što i predstavlja
prvu kosmièku brzinu.
Znaèi ukoliko
želimo da pošaljemo
neki satelit u kružnu orbitu na visini od
recimo 200 km od Zemljine površine, moraæemo
da mu saopštimo brzinu od 7,79 km/s. Kao
što vidimo prva kosmièka
brzina nije konstanta nego ima razlièite
vrednosti za razlièite polupreènike
orbite na kojima se satelit kreæe (i
naravno za razlièite planete). Takoðe
treba pomenuti da æe orbita satelita koji
kruži na nekoj visini postajati izduženija,
odnosno elipsasta ukoliko mu na toj visini saopstimo veæu
brzinu.
Ako satelitu nastavi da se poveæava
brzina, on æe u jednom trenutku imati
toliku brzinu da æe moæi
da se oslobodi gravitacionog uticaja tela oko kojega je kružio.
I brzina koju satelit u tom trenutku ima se naziva
drugom kosmiækom brzinom.
Ona se izvodi na sledeæi naèin:
letelica koja se udaljava od nekog tela (Zemlje na primer), ima
energiju E koja se može napisati kao:
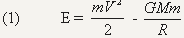
gde je prvi èlan
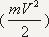 kinetièka
energija tog tela, a drugi kinetièka
energija tog tela, a drugi
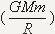 njegova potencijalna
energija. Ako se ta letelica potpuno oslobodi uticaja Zemljinog
gravitacionog polja, onda bi moglo da se pretpostavi da R teži
beskonaènosti, odnosno da mu je
potencijalna energija nula u tom trenutku. Takoðe
ako pretpostavimo da je imala minimum energije koji je potreban za
ovo, odnosno da je svu energiju potrošila
na oslobaðanje iz Zemljinog gravitacionog
polja, brzina, a samim tim i kinetièka
energija, bi na kraju trebale da su jednake nuli. A to sve ukazuje
da je i ukupna energija jednaka nuli. Ako uzmemo u obzir zakon održanja
mehanièke energije formalno napisano to sve
izgleda ovako: njegova potencijalna
energija. Ako se ta letelica potpuno oslobodi uticaja Zemljinog
gravitacionog polja, onda bi moglo da se pretpostavi da R teži
beskonaènosti, odnosno da mu je
potencijalna energija nula u tom trenutku. Takoðe
ako pretpostavimo da je imala minimum energije koji je potreban za
ovo, odnosno da je svu energiju potrošila
na oslobaðanje iz Zemljinog gravitacionog
polja, brzina, a samim tim i kinetièka
energija, bi na kraju trebale da su jednake nuli. A to sve ukazuje
da je i ukupna energija jednaka nuli. Ako uzmemo u obzir zakon održanja
mehanièke energije formalno napisano to sve
izgleda ovako:
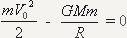 , ,
gde je V0
poèetna
brzina letelice, a R polupreènik sa kojega
je letelica lansirana. Dalje ovu jednacinu mozemo napisati kao:
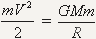 , ,
pa zatim i skratiti m i dobiti:

što i predstavlja
izraz za raèunanje druge kosmièke
brzine. Druga kosmièka brzina za letelice
koje su lansirane sa površine Zemlje iznosi
približno 11,2
km/s. Za ostale planete
æe naravno biti drugaèija, jer u
formuli za drugu kosmièku brzinu figurišu
masa i polupreènik planete koja se posmatra
(oni su naravno razlièiti od sluèaja
do sluèaja). Treba i primetiti da se prva i
druga kosmièka brzina razlikuju samo za
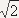 ,
što bi znaèilo da
ako hoæemo da neki satelit u kružnoj
orbiti pošaljemo van uticaja gravitacionog
polja u kome se nalazi treba samo da mu poveæamo
brzinu za ,
što bi znaèilo da
ako hoæemo da neki satelit u kružnoj
orbiti pošaljemo van uticaja gravitacionog
polja u kome se nalazi treba samo da mu poveæamo
brzinu za
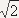 . .
Da bismo objasnili šta
je parabolièna brzina, odnosno zašto
se tako zove moramo baciti pogled na formulu (1) još
jednaput. Naime u formuli (1) ukoliko je vrednost E < 0, onda je
putanja tela kružnica ili elipsa, ukoliko
je E = 0, onda je putanja tela parabola, a ako je E > 0, onda je
putanja hiperbola. Ako imamo u vidu da je brzina koju telo ima
kada je E = 0 druga kosmièka brzina postaje
jasno da je ona isto što i prabolièna
brzina, tj. da se zbog oblika putanje koju telo ima pri drugoj
kosmièkoj brzini ona zove još
i parabolièna brzina.
Da bismo još malo
pojasnili izgled putanje i vezu sa energijom uzeæemo
primer tela koje uleæe u Sunèev
sistem. Ukoliko je telu E < 0, ono æe
ostati zarobljeno Sunèevom gravitacijom u
kružnoj ili eliptiènoj
orbiti. Dalje ukoliko mu je E = 0, ono æe
proæi oko Sunca i onda opet napustiti Sunèev
sistem i putanja æe mu imati oblik slova U
(iliti parabole – neke komete imaju ovaj oblik putanje). Ukoliko
je E > 0 za to telo, ono æe proæi
kroz Sunèev sistem i putanja
æe mu imati oblik ) (iliti hiperbole).
Treæa kosmièka
brzina predstavlja zapravo brzinu potrebnu da se neko telo
lansirano sa Zemlje (recimo) oslobodi Sunèeve
gravitacije. Letelici lansiranoj sa Zemlje bi treæa
kosmicka brzina iznosila 16,7 km/s.
Èetvrta
kosmicka brzina je brzina potrebna da
se neko telo (lansirano iz Sunèevog
sistema) oslobodi gravitacije cele Galaksije, odnosno Mleènog
Puta. Iako se navode razne vrednosti (reda 290 km/s), zapravo se
još uvek pouzdano ne zna kolika bi ona
mogla da bude. Ovo je posledica èinjenice
da mi još uvek ne znamo precizno masu
Galaksije*.
Kosmièke brzine
predstavljaju njutnovski koncept koji je razvijen još
tokom 17. i 18. veka. Tokom sedamdesetih godina 20. veka je recimo
pronaðen rad Džona
Mièela, engleskog nauènika
iz 18. veka, koji je zainteresovan idejom brzine potrebne da se
napusti neka planeta ili masivno telo, zakljuèio
da bi moglo da postoji telo kome bi ta brzina (druga kosmièka)
bila jednaka ili veæa od brzine svetlosti.
I samim tim prvi dosao na ideju da bi mogle da postoje crne rupe.
* Uzgred budi receno ukoliko se piše
Galaksija sa velikim slovom misli se na našu
galaksiju, tj. Mleèni Put. Ukoliko se piše
malim slovom misli se na astronomski objekat.
Što se tièe
najmanje brzine doleta na Mesec stvarno ne znam kolika bi ona
bila. Pretpostavljam da bi brzina koju bi trebalo saopštiti
letelici tokom poletanja morala da bude bar druga kosmièka
brzina. U svakom sluèaju sama brzina
letelice se tokom ulaska u orbitu oko Meseca koriguje da bi se
postigla željena visina. Lender koji se
odvaja od letelice i sa lunarne orbite spušta
na površinu Meseca ne sme da preðe
odreðenu brzinu koja predstavlja maksimalnu
bezbednu brzinu za spuštanje, da ne bi
povredio astronaute tokom sletanja ili se oštetio
toliko da onemoguæi ponovno poletanje sa
Meseca (logièno). Ova brzina naravno zavisi
od mnogo faktora, od kojih se veæina odnosi
na sam kvalitet izrade lendera i tehnologiju koja se koristi
prilikom spuštanja.
I za kraj par napomena. Ukoliko budeš
koristio Internet ili stranu literaturu na
engleskom da saznas više o ovim pojmovima,
bilo bi korisno da imaš u vidu da se na
engleskom koristi izraz "escape velocity"
za drugu kosmièku brzinu. Za prvu koriste
izraz "circullar velocity".
Za treæu i èetvrtu
nisam siguran kako ih taèno zovu, ali
verujem da æeš
uspeti to da saznaš ako budeš
bio dovojno uporan.
U svakom sluèaju
želim ti puno sreæe
u tvom daljem bavljenju astronomijom i astronautikom i nadam se da
ti je ovaj odgovor donekle pomogao i zadovoljio tvoju
radoznalost...
Vedro nebo,
Nemanja
Martinoviæ
|