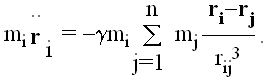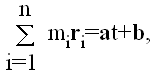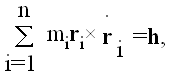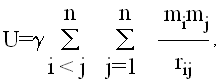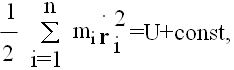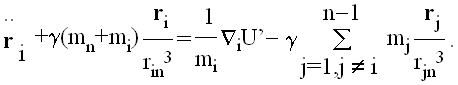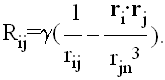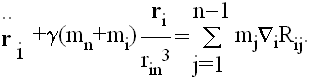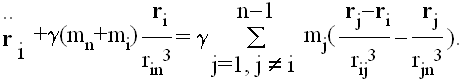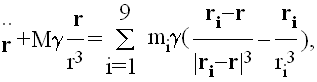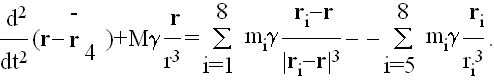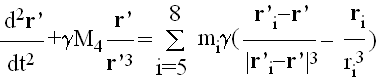Haos u kretanju asteroida u Sunčevom sistemu

Zlatko Papić ¹

Matematička gimnazija, Beograd

2000 Maj

APSTRAKT

Ovde je predstavljen jedan aspekt haosa u prirodi koji se odnosi na dinamiku planetarnih sistema i kretanje malih tela u njima. Usled analitičke nerešivosti datog problema i poteškoća koje se u tom prilazu javljaju (poglavlje 1), izvršena je numerička integracija orbita 10 asteroida u intervalu od 10 miliona godina i rezultati predstavljeni, zajedno sa nekim mogućim uzrocima haosa koji je pri tome uočen, kao i uloga i značaj sopstvenih elemenata malih planeta (poglavlje 2). Na kraju (poglavlje 3), navedene su i neke od primena haosa u nebeskoj mehanici (ocena starosti asteroidnih familija, dinamika potencijalno opasnih asteroida, transport kosmičkog materijala, meteorita i asteroida, do Zemlje).

1 Uvod: o problemu N tela

U ovom poglavlju će biti ukratko predstavljene jednačine problema N tela, njihova poznata resenja, kao i metode pomoću kojih se do nepoznatih resenja teorijski i praktično (do na odredjenu, zadatu, tačnost) može doći.

Neka se sistem N tela sastoji od materijalnih tačaka masâ m_i i radijus-vektorâ r_i, gde je i=1,2,..,n, i r_i su izrazeni u odnosu na inercijalni referentni sistem. Neka je

tada je jednačina kretanja tela m_i

Sumiranje isključuje slučaj j=i, što bi proizvelo neodredjenost razlomka, te ovo ubuduće neće biti naglašavano. Ovaj sistem diferencijalnih jednačina je nemoguće rešiti u konačnoj formi jer je potrebno poznavati 6n skalarnih integrala, od čega je, u stvarnosti, moguće odrediti 10.

Ako se saberu sve jednacine oblika (1), svi članovi na desnoj strani će se skratiti, i imaćemo

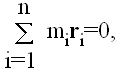
Ovo se može odjednom integraliti, pri čemu se dobija

gde su a i b konstantni vektori. Relacija (2) znaci da se centar mase sistema kreće, u odnosu na (inercijalni) referentni sistem, pravolinijski i konstantnom brzinom. Stoga možemo uzeti koordinatni početak u centru mase sistema, gde je

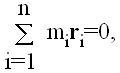
i jednacine (1) će i dalje vaziti.

Pomnožimo li (1) vektorski sa r_i× i saberemo dobijenih n jednačina, svi članovi na desnoj strani se skraćuju, i dobijamo

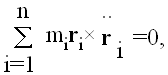
ili

gde je h konstantni vektor. Ovo je takozvani integral "površina."

Ravan kroz centar mase, upravna na h, naziva se invarijabilnom ili Laplaceovom ravni sistema. Kada se ova analiza primenjuje rigorozno na fizički sistem treba biti oprezan. Integral ugaonog momenta je rezultat izolovanosti sistema, odnosno odsustva spoljašnjih sila i odražava činjenicu da je ukupan moment impulsa konstantan; on potiče od orbitalnih revolucija planeta i rotacija oko sopstvenih osa. Ako su sva tela čvrsta, sferno-simetricna i medjusobno izolovana, postojaće i invarijabilna ravan. U suprotnom, precesiona kretanja i efekti plimskog trenja dovešće do razmene momenta impulsa, pa će se h, kako je definisano u (3), menjati sa vremenom. Ipak, gornji uslovi su približno ispunjeni za naš planetarni sistem i u praksi možemo govoriti o invarijabilnoj ravni Sunčevog sistema: ona otprilike ima elemente W = 107⁰ i i=1⁰35^ó, u odnosu na ravan ekliptike.

Dalje, moze se definisati U, funkcija sile sistema, kao

gde se uzima tačno jedno ponavljanje svake od kombinacija masâ m_i i m_j. Onda je komponentna sile odredjena sa

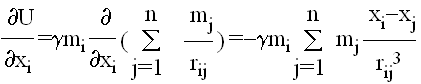
Odavde je moguće zapisati jednačinu (1) kao

gde je

Pretpostavimo da želimo iznova organizovati naš sistem N tela. Počnimo sa m₁ na položaju r₁. Pri premeštanju tela m₂ iz beskonačnosti do r₂ vrši se rad

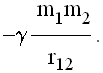
Ako se sada premesti m₃ na r₃, dodatni rad iznosi

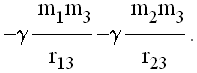
Ponavljajući prethodni postupak, vidi se da -U predstavlja ukupnu potencijalnu energiju sistema.

Pomnozimo sada (5) skalarno sa  i saberimo svih n jednačina:

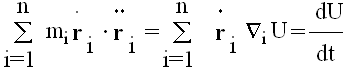
Integraljenjem ove relacije dobija se:

što je integral energije. Neka je T kinetička energija sistema. Tada je

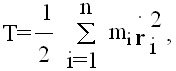
i integral energije se može zapisati kao

što predstavlja desetu konstantu integracije i kompletira analitička rešenja najopštijeg problema kretanja medjusobno interagujućeg sistema N izolovanih tela koja je principijelno moguće dobiti.

Činjenica da je sistem N tela nerešiv, ipak ne daje odgovor na pitanje da li je dati sistem (a cilj je, pre svega, pronaći odgovor za Sunčev sistem) stabilan ili ne. Fundamentalni radovi Laplasa (Laplace) i Lagranza (Lagrange) dokazali su analitički da se planete kreću kvaziperiodično, do prvog reda po masama (u jednačinama kretanja), ekscentričnostima i nagibima planetskih putanja², pa je glavni cilj nebeske mehanike 19. veka bio u konstruisanju kvaziperiodičnih rešenja za tela u Sunčevom sistemu pomoću računa poremećaja. Kasnije, Poankare (Poincaré) pokazuje da pošto je moguće formalno prikazati rešenja planetarnih jednačina kretanja u obliku beskonačnih redova, tada ovi redovi u opštem slučaju nisu konvergentni. U drugoj polovini ovog veka, na osnovu KAM³ teoreme, je zaključeno da ako su poremećaji mali, odnosno mase, ekscentričnosti i inklinacije planeta dovoljno male⁴ , onda veliki broj početnih uslova dovodi do kvaziperiodičnih rešenja. Sunčev sistem sasvim sigurno ne zadovoljava kriterijume ove teoreme. Ipak, naglo povećanje performansi računara, imalo je preponderantni uticaj na drugi, numerički, pristup problemu. Veliki broj obimnih simulacija dinamike Sunčevog sistema u poslednjih 10 godina samo je potvrdio njegovu haotičnost i gubitak prediktabilnosti već nakon 100 miliona godina⁵ (poremećaj reda velicine 10te znacajne cifre početnih uslova doveo bi do 100 % odstupanja nakon tog vremenskog perioda i rešenje bi izgubilo svoj fizički smisao). Naravno, to ne znači da će posle navedenog vremena doći do katastrofalnih dogadjaja kao, na primer, presecanja orbita Zemlje i Venere, već da tradicionalne metode nebeske mehanike ne mogu tačno da predvide polozaje i brzine tela Sunčevog sistema. Ipak, njegova velika starost (kao i starost i istorijski dosije planete Zemlje) decentno ukazuju na znatan nivo stabilnosti.

Pošto je, dakle, isuviše složeno manipulisati Sunčevim sistemom takvim kakav je, odredjene aproksimacije u numeričkom pristupu se moraju primeniti. To se najčešće svodi na kompromis izmedju brzine izvršavanja programa i željene tačnosti. Stoga je vrlo važno izvorni problem teorijski uprostiti koliko god je to dopustivo.

Pretpostavimo da je, kao što je to slučaj sa Suncem u našem planetarnom sistemu, jedna masa, m_n, dominantna. Uzmimo koordinatni pocetak u centru m_n; neka je vektor položaja tela m_i u novom sistemu r_i’. Tada je

Vrednosti r_ij se ovom transformacijom ne menjaju, pa je itd. Sada je

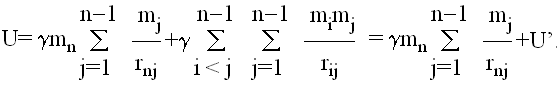
Dalje,

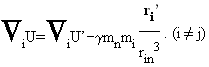
Iz jednačine kretanja tela m_n se dobija:

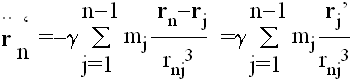
Jednačina kretanja tela m_i glasi

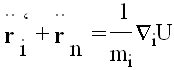
ili

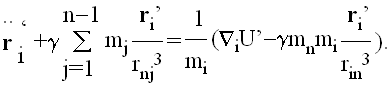
Prebacimo li itičlan ispred sume, dobija se:

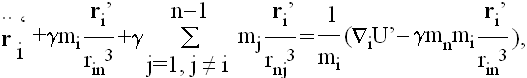
ili, preimenovanjem promenljivih r_i’ sa r_i, što se sme uraditi pošto se sada u potpunosti nalazimo u novom referentnom sistemu,

Neka je sada

Onda je

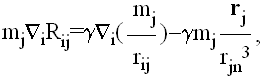
i

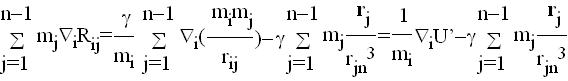
Kombinujući ovaj rezultat sa (7), dobijamo

Jednačine (9) su fundamentalne. Ako su R_ij jednaki nuli, sve se svodi na (prost) slučaj kretanja dva tela, pa su upravo R_ij članovi “odgovorni” za sve poremećaje i razlike u odnosu na keplerovsko kretanje. Oni se zato i zovu funkcijama poremećaja.

Napomenimo samo da se jednacina (9) moze napisati u sledećem obliku:

Prvi član na desnoj strani prethodne jednačine predstavlja direktne uticaje poremećajnih tela na telo m_i; drugi član označava indirektne uticaje, koji se vrlo često (pogrešno) zanemaruju, a predstavljaju uticaj velikih planeta na koordinatni početak.

U slucaju asteroida⁶ u Sunčevom sistemu, jednacina (10) poprima sledeći oblik

gde je M- masa Sunca, r-vektor položaja tela, a sumiranje se vrši po devet velikih planeta⁷ i povećanju njihovih srednjih udaljenosti od Sunca (koordinatni početak je uzet u centru Sunca), pri čemu i=1 odgovara Merkuru itd.

Osim ako telo ne prolazi blizu neke planete, najveći doprinos desnoj strani jednačine (11) potice od Jupitera, m₅, dok su efekti ostalih planeta relativno mali. Ova aproksimacija proizilazi iz činjenice da je najveći broj asteroida skoncentrisan na lokaciji tzv. Glavnog asteroidnog pojasa, ilustrovanoj na slici 7, koji se proteže izmedju orbita Marsa i Jupitera. U slucaju transneptunskih asteroida, najveći doprinos desnoj strani jednačine (11) potiče od Neptuna i tako dalje, u zavisnosti od konkretnog problema. Sledi da je u praksi i neophodno i moguće pojednostaviti (11), s tim što je svaki korak potrebno teorijski potkrepiti.

Uticaj Plutona se može sasvim zanemariti zbog njegove male mase (nekoliko redova veličine manje od mase velikih spoljašnjih planeta) i velike udaljenosti. Ovo nije slučaj kod Merkura gde se indirektni članovi u (11) ne mogu zanemariti; oni imaju oblik:

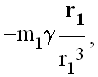
što je ekvivalentno sa

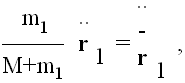
gde je centar mase Sunca i Merkura. Odatle se (11) moze napisati kao

 
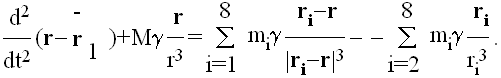
U praktičnom radu često je vrlo pogodno zanemariti i sve četiri unutrašnje planete pošto su njihove direktne perturbacije male⁸, a indirektne se mogu apsorbovati baricentričnom popravkom, odnosno prelaskom u sistem sa koordinatnim početkom u centru mase Sunca i planeta Zemljinog tipa. Ako je ova tačka odredjena sa , onda
 

Ako je telo dovoljno daleko od četiri unutrašnje planete za r >> r_i, i=1,2,3,4, onda

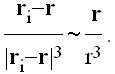
Takodje, r4 je uvek malo, manje od 5 ×10^-6 AJ, pa se za veliko r moze uzeti

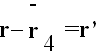
i

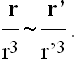
Neka je

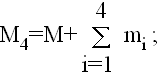
tada jednačina (11) glasi:

Model Sunčevog sistema (koji je korišćen u ovom radu u okviru softverskog paketa ORBIT9x) zasniva se na gore pomenutoj analizi, odnosno uključuje direktne poremećaje svih velikih planeta, simultano izračunavajući njihove orbite zajedno sa orbitama probnih telâ. Unutrašnje planete su izostavljene iz direktne integracije, ali je primenjena baricentrična popravka na početne uslove, što, u principu, pokriva 90 % indirektnih efekata (vidi Milani i Knežević, 1992). ORBIT9x koristi precizan multistep integrator (za početne korake se koristi simplektički Runge-Kutta metod) i omogućava praćenje orbita tela u, pre svega, Sunčevom sistemu, u okviru različitih dinamičkih modela i dugih vremenskih intervala. Eksperimentalni uzorak za svrhu ovog rada uključuje 10 numerisanih, realnih, asteroida čiji su orbitalni elementi preuzeti od Minor Planet Centra i stoga se mogu smatrati preciznim (provereni astrometrijskim posmatranjima u više opozicija).

Literatura

[1] Danby,J.M.A.: Fundamentals ofčelestial Mechanics, 2nd edition, 1988, Richmond:Willman-Bell
[2] Laskar,J.: A numerical experiment on thečhaotic behaviour of the Solar system,
Nature, vol.338
[3] Knezević,Z.:čhaos in the motion of asteroids, 1999
[4] Knezević,Z.: Proper elements of minor planets, Publ. Obs. Astron. Belgrade No. 48 (1995), 7-30
[5] Milani,A.,Nobili,A.M.,Knezević,Z.: Stablečhaos in the asteroid belt, 1997, Icarus 125, 13-31
[6] Rabinowitz, D., Helin, E., Lawrence, K., Pravdo, S.: Nature 403, 165-166
[7] Applied Physics Laboratory, Johns Hopkins University, NEAR Mission Status, http://near.jhuapl.edu 

Fusnote:

¹Murmanska 4, 11 160 Beograd, tel. 3406476, 426015, E-mail: papicz@EUnet.yu

²S obzirom na to da su odgovarajući odnosi masâ planeta i Sunca reda veličine m = m_i/M ~ 10^-3 do 10^-9, a odgovarajuće ekscentričnosti i nagibi putanja (u radijanima) reda 10^-2, odgovarajući članovi u razvoju koji sadrže drugi i više stepene ovih veličina su zanemarljivi

³Kolmogorov-Arnol'd-Moser

⁴Pod "dovoljno malim" se podrazumeva da vrednosti odgovarajućih m, e, i treba da budu svakako ispod 10^-43, sto, evidentno, nema nikakav praktični znacaj!

⁵Ova procena je relativno paušalna, pošto različiti delovi Sunčevog sistema pokazuju drastične razlike po pitanju stabilnosti. (videti dalje u tekstu)

⁶Pod 'asteroidom' (sin. mala planeta) se podrazumeva planetoidno telo malih dimenzija, do oko 1000 km u prečniku

⁷U ovom razmatranju Pluton je smatran jednom od velikih planeta.

⁸Osim toga, uključivanje npr. Merkura u simulaciju bi zahtevalo upotrebu vrlo malog vremenskog koraka da bi se greška numeričke metode držala u granicama tolerancije, analogno važi i za sistem Zemlja-Mesec, itd.

vrh