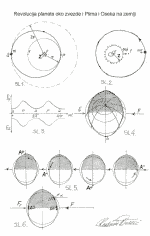
Revolucija
planete oko zvezde
i plima i oseka na Zemlji
|
I UVOD
Kruženje ili revolucija planete oko zvezde je objašnjena Keplerovim i Newtonovim zakonima. Prema Newtonovom zakonu gravitacije, kruženje planete oko zvezde je posledica uravnoteženja; gravitacione sile kojom zvezda privlači planetu i radijalne – centrifugalne sile koja teži da planetu udalji od zvezde. Keplerovi zakoni daju preciznu predstavu o kretanju planete pri revoluciji oko zvezde, i to;
1. Planete opisuju oko Sunca eliptične putanje; u zajedničkoj žiži tih elipsa nalazi se Sunce.
2. Radius vektor povučen od Sunca do planete prevlači u jednakim delovima vremena jednake površine.
Fundamentalno svojstvo drugog Keplerovog zakona je važenje zakona o održanju momenta impulsa (L).
L = r m v = const.
Ovo znači, da se konstantna masa planete (m), kreće promenjivom brzinom (v) na promenjivom udaljenju - radijus vektoru (r) od zvezde.
Ovako , uopšteno prikazano izgleda priroda revolucije planete oko zvezde, koja je pre četiri stotina godina Keplerovim, a sto godina kasnije Newtonovim zakonima „definitivno“ objašnjena. Ovaj rad će diskutovati i probati da razjasni fenomen revolucije planete oko zvezde na takodje veoma prirodan način, srodan prihvaćenom i uvaženom načinu.
II ANALIZA II KEPLEROVOG ZAKONA
Prema II Keplerovom zakonu radijus vektor povučen od Zvezde do planete prevuče jednaku infinitezimalnu površinu dS u infinitezimalnom delu vremena dt, pa se može predstaviti u obliku:
dS/dt = const.
Takodje, fundamentalno svojstvo II Keplerovog zakona je i važenje zakona o očuvanju momenta impulsa (L)
L = r m v = const.
(m) je konstantna veličina i predstavlja masu planete, dok su radijus vektor ( r ) i vektor brzine ( v ) kretanja planete, promenjive veličine. Tamo gde je na putanji planete radijus vektor ( r ) minimalan (perihel) vektor brzine ( v ) je maksimalan i obratno u afelu je radijus vektor ( r ) maksimalan a vektor brzine ( v ) minimalan.
Očigledno je da planeta u toku revolucije oko zvezde eliptičnom putanjom, neprestano menja svoj moment inercije ( I ).
I = m r²
Tako se ima da je moment inercije planete pri revoluciji oko zvezde najveći u afelu ( Ia ) a najmanji u perihelu ( Ip ) putanje. To za posledicu ima i neprestanu promenu ugaone brzine (ω) revolucije planete jer mora, prema napred iznetom, važiti zakon o održanju momenta impulsa:
L = I ω = const.
I iz poslednjeg izraza je jasno da za najmanji moment inercije (perihel), planeta pri revoluciji oko zvezde ima maksimalnu ugaonu brzinu, dok za najveći moment inercije (afel) planeta ima minimalnu ugaonu brzinu. Očigledno da neprestano dolazi do transformacije momenta impulsa planete i da je to od najvećeg značaja za revoluciju planete oko zvezde i slična kretanja u prirodi.
III TRANSFORMACIJA MOMENTA IMPULSA GENERIŠE ENERGIJU
Moment impulsa planete je konstantna veličina iako se neprestano u toku revolucije planete menjaju vrednosti momenta inercije ( I ) i ugaone brzine ( ω ). Praktično se na račun smanjenja jedne fizičke veličine povećava i to linearno ona druga i obratno. Takva promena vrednosti biće nazvana: transformacija momenta impulsa. Posledice koje ona proizvodi biće analizirane sledećim računom.
Kinetička energija planete, srodno izračunavanju energije kod rotacionog kretanja, data je izrazom;
E = ½ I ω²
Na primeru putanje prikazanoj slikom Sl. 1. će biti razmotren energetski bilans sistema , planeta – zvezda:
Neka je eliptična putanja drastično velikog ekscentriciteta i neka u njenoj jednoj žiži stoji zvezda. Odredjeno je udaljenje planete mase (m) od zvezde u afelu i iznosi 2r pri ugaonoj brzini kretanja planete ω. Moment inercije planete u afelu je:
Ia = m ( 2r )² ,
pa je moment impulsa planete u afelu dat izrazom:
L = Ia ω = m (2r)² ω = m 4 r² ω
Udaljenje planete od zvezde u perihelu putanje iznosi r. Moment inercije planete u perihelu je:
Ip = m r²
Kako važi zakon o održanju momenta impulsa to je moment impulsa konstantan i u afelu i u perihelu.
Ia ω = Ip ω´ = m r² 4ω = m r² ω´
Ugaona brzina planete u perihelu, za ovaj primer, iz ove jednačine iznosi: ω´ = 4 ω
Moment inercije planete u perihelu je jednak četvrtini momenta inercije u afelu: Ip = Ia/4
Kinetička energija planete u afelu je: Ea = ½ Ia ω², dok je u perihelu putanje
Ep = ½ Ip (ω´)² = ½ (Ia/4) (4 ω)² = 4 Ea
Pri revoluciji planete oko zvezde, transformacijom momenta impulsa, kinetička energija joj se povećala za četiri puta u perihelu u odnosu na kinetičku energiju koju je imala u afelu putanje. Ovo povećanje energije je zapravo rad kojeg vrši gravitaciona sila zvezde protiv centrifugalne sile koja teži da planetu odvuče sa putanje.
Kinetička energija planete u perihelu putanje se mora negde i utrošiti. To se zaista i dogadja jer kada planeta ponovo dodje do afela putanje tokom revolucije po opisanoj drastično ekscentričnoj putanji , energija joj četiri puta opadne. Prema činjenici da mora važiti i zakon o održanju energije, jasno je da se energija generisana transformacijom momenta impulsa planete utrošila na pomeranje zvezde, koja se kreće tako da se može reći : centar mase zvezde se kreće eliptičnom putanjom , proporcionalno manjih osa, Sl. 2.
IV INTERAKCIJA PLANETA – ZVEZDA
Mora važiti Newtonov zakon akcije i reakcije. Znači, koliko zvezda privlači planetu, isto toliko i planeta privlači zvezdu, u svakom trenutku u toku revolucije planete. Srodno tome, mora važiti i zakon o održanju impulsa. Planeta „pada“ ka zvezdi trenutnom brzinom υ pa je njen trenutni impuls interakcije: p = m υ
Zvezda mase M teži da se pokrene ka planeti trenutnom brzinom υ´ pa joj je trenutni impuls interakcije: p´ = M υ´.
Kako mora važiti u svakom trenutku zakon akcije i reakcije ima se: p = p´; m υ = M υ´,
Odakle je trenutna brzina kretanja zvezde: υ´ = (m/M) υ .
S obzirom na odnos masa zvezde i planete, iz poslednjeg izraza je jasno da je brzina kretanja zvezde ekstremno mala, ali da dokazuje da ogromna masa zvezde prelazi odredjeni put na kome se troši kinetička energija planete generisana transformacijom momenta impulsa.
Ova „vuča“ zvezde se manifestuje, u ovom ekstremnom slučaju gde je putanja velikog ekscentriciteta i gde se razmatra revolucija samo jedne planete, kao opisivanje centrom mase zvezde jedne elipse čija se jedna geometrijska žiža poklapa sa geometrijskom žižom putanje planete, a koja je „izdužena“ ka perihelu planetarne putanje. Slika Sl. 2. prikazuje putanju centra mase zvezde a slika Sl. 3. uporedni dijagram promene kinetičkih energija planete i zvezde. Ukupna proizvedena kinetička energija transformacijom momenta impulsa planete jednaka je ukupnoj količini kinetičke energije potrebne za „vuču“ zvezde.
U svakodnevnom životu analogija ovom primeru je efekat razbalansiranog točka na vozilu. Naime, ako se dogodi da sa točka otpadne komadić olova od 50 grama, kojim je točak izbalansiran, pri odredjenim brzinama se ima da čitavo vozilo mase nekoliko tona počne da vibrira i da trese, što se zapravo dogadja zvezdi.
Prema I Keplerovom zakonu kretanje planete po eliptičnoj putanji za posledicu ima neprestano menjanje vektora brzine v i radijus vektora r udaljenja planete od zvezde, dok joj moment impulsa ostaje konstantan prema II Keplerovom zakonu .
Impuls planete p = m v , zbog neprestane promene brzine kretanja se neprestano menja u vremenu:
d (m v)/d t = F
Što je opšti oblik II Newtonovog zakona sile i ubrzanja. Kako planeta poseduje konstantnu masu (m) to možemo ovu jednačinu izraziti i kao:
m (d v)/d t = m a = F
Na planetu stalno deluje promenjiva sila F u smeru i pravcu njenog kretanja, te se tokom njene revolucije po eliptičnoj putanji kreće promenjivom brzinom v pod dejstvom promenjivog ubrzanja a.
Iz svega napred navedenog proizlaze sledeći zaključci.
1. Kretanje planete eliptičnom putanjom oko zvezde, na račun rada privlačne gravitacione sile, izaziva proizvodnju kinetičke energije planete modelom transformacije momenta impulsa.
2. Proizvedena kinetička energija planete se troši na pokretanje ( vuču ) zvezde oko koje planeta kruži, tako da centar mase zvezde kruži eliptičnom putanjom suprotno izduženoj i proporcionalno, za količnik masa M/m puta umanjenom, od putanje planete.
3. Kinetička energija kruženja planete i kinetička energija uložena u kretanje (vuču) zvezde moraju na kraju jednog ciklusa ( godine ) biti jednake.
4. Kretanje sistema planeta oko zvezde izaziva kruženje ( vuču ) zvezde po putanji koja je rezultat superpozicije svih pojedinačnih interakcija planeta – zvezda.
5. Na planetu stalno deluje promenjiva sila u pravcu i smeru putanje njene revolucije.
6. Nemoguće je kruženje nebeskih tela po apsolutno kružnoj putanji.
V PLIMA I OSEKA NA PLANETI ZEMLJI
Nastanak plime i oseke na planeti Zemlji je prirodna pojava koja se može objasniti prema do sada iznetom, kao posledica Zemljine revolucije oko Sunca i njene rotacije oko sopstvene ose. Ujedno, pojava plime i oseke je svojevrstan dokaz ranije iznetih analiza i zaključaka o revoluciji planeta oko zvezde. Posebno je važan, ranije navedeni, peti zaključak za razumevanje prirode nastanka plime i oseke, koji glasi:
5. Na planetu (Zemlju) stalno deluje promenjiva sila u pravcu i smeru putanje njene revolucije.!
Kada putnik u automobilu koji polazi iz stanja mirovanja u ruci drži čašu vode i posmatra njenu površinu, primetiće da se u početku (mirovanju) ravna – vodoravna površina vode podiže ka zadnjem zidu čaše i da se sve dok traje ubrzavanje automobila takvo stanje održava. Kada automobil postigne željenu brzinu i nastavi da je održava, ponovo će površina vode (tečnosti) u čaši postati vodoravna. Kada automobil, ne menjajući brzinu udje u krivinu, ponovo će se voda u čaši podići prema smeru i pravcu trenutnog radijusa krivine.
Iz ovog empirijskog razmatranja, već veoma dobro poznatog primera, mogu se izvući sledeći zaključci;
- Masa vode (tečnosti) u čaši se deformiše pri ubrzavanju.
- Deformacija vode je takva da se javlja težnja tečnosti za skraćenjem dimenzije koju je zauzimala u smeru kretanja (dužine).
- Iz razloga nestišljivosti, vode (tečnosti), dolazi do težnje produženja – povećanja ostalih dimenzija njene zapremine (širine i visine).