|
| nastavak |
|
<< prethodna strana | 1 | 2 | |
Deo 3.
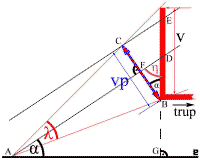
Dosadašnja razmatranja su za predmet u jednoj ravni. Ostaje da razmotrimo predmet u trećoj dimenziji, po visini. Posmatrajmo sliku 31. Crvena traka sa desne strane predstavlja zadnji deo aviona, a duž BDE je njegov rep. Posmatrač u tački A vidi rep aviona pod nekim uglom, recimo λ, i zbog toga on rep dužine v između tačaka B i E, vidi kraći kao vp – prividna visina repa što je duž između tačaka B i C. Kako je po pravilu uglova sa normalnim kracima ugao DAG jednak uglu DBF, to je ugao između v i vp jednak uglu α. Ili, može i ovako: u pravouglom trouglu AGD, ugao η kod temena D je 90-α, pa je u pravouglom trouglu BFD ugao kod temena B ugao α. Sada, u pravouglom trouglu BCE važi:
cos(α) = vp / v, pa iz ovoga sledi:
vp = v * cos(α).
|
Kliknite na ilustraciju |
 |
|
Slika 31 |
 |
|
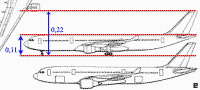
Slika 32 |
 |
|
Slika 33 |
Dakle, ako bi znali visinu repa aviona v, znali bi i njegovu prividnu visinu vp, slika 31. Visina repa aviona v je otprilike 50% ukupne visine aviona u referencama, slika 32. Kako je kod putničkih aviona visina samog repa 5-10 metara, to znači da bi gore spomenutoj prividnoj dužini aviona dp (slika 22.) morali dodati koji metar, na primer kao na slici 33.
Naravno, vp se menja u zavisnosti od rastojanja AD (slika 31.), rep aviona posmatraču može biti bliži ili dalji a da ostane na liniji AD i pod uglom α u odnosu na posmatrača, ali gornji kosinus uvek ostaje.
Ne razmatram množenje vp sa nekim dodatnim sinusom ili kosinusom koje bi nastalo od naknadnog skraćenja visine slično kao i skraćenje širine na slici 21., tj. ne posmatram visinu aviona iz druge ravni koja bi bila normalna na prvu, kao što sam posmatrao dužinu aviona. Smatram da vertikala sve vreme ostaje ista, jer se avion uglavnom kreće i blago okreće u horizontalnoj, dakle jednoj ravni. Neko dodatno skraćenje vertikale u odnosu na posmatrača bi se dogodilo samo onda kada bi se avion nagnuo, bilo na bok, bilo da pikira, bilo da uzleće, što ovde nije slučaj.
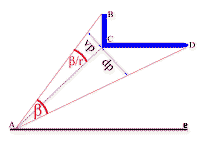
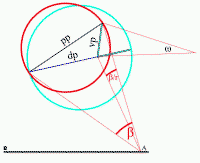
Ali, na slici 33. nacrtan je samo poseban slučaj kada posmatrač gleda avion tačno u rep, tj. kada su osa aviona CD i pravac AC između posmatrača i aviona u istoj ravni, kao na slici 11. Realan slučaj, i to baš kao na Ayiomamitis-ovoj slici bi bio kao na slici 34: dp (plava linija) zauzima najveći deo vidnog ugla β (to je crveni krug), vp (tirkizna linija sa crnom ivicom) zauzima neki manji deo β/r, a prečnik vidnog ugla je pp – prividni poluprečnik, koji jako liči na hipotenuzu aviona dh sa slike 41. ali nije, jer ovde na slici 34. su dp, vp i pp u istoj ravni, u crvenom krugu koji oivičava vidni ugao β, a prava, fizička dh od aviona sa slike 41. je pod uglom negde iza tog crvenog kruga. Avion je svojom uzdužnom osom pod uglom na ravan koja je normalna na pravac posmatranja, a u toj ravni su prividne veličine: dp, vp i pp. Na žalost, tu je kraj: pomoću ove slike 34., možemo samo da shvatimo prostorni raspored pravih i prividnih veličina aviona. Iako znamo koliko je dp i vp, ipak ne znamo koliko je β/r, niti koliko je pp, jer dp i vp u opštem slučaju ne grade pravougli trougao. Možda neko nađe rešenje i za ovaj problem.
|
Kliknite na ilustraciju |
 |
|
Slika 34 |
Tako da ja smatram da je potrebno uzeti da je prava prividna dimenzija aviona (normalna na pravac posmatranja) pp (slika 34.) zapravo negde na sredini između slučaja kada je pp = dp i slučaja kada je pp = dp+vp. Ovaj drugi slučaj je nacrtan na 2 slike: na slici 33. kada se dve plave linije dp i vp sabiraju, i na slici 34. slučaj kada je vp zarotirana naniže, sabira se sa dp i čini veći, tirkizni vidni ugao. U ovom drugom slučaju sa većim vidnim uglom na slici 34., sama vp čini deo vidnog ugla ω koji je veći od ugla β/r.
Slučaj pp = dp već imamo, to je dpukupno na kraju dela 2. A slučaj pp = dp + vp je sledeći. Za avione dužine 50 m, visina samog repa v (slika 31.) je minimalno oko 7 metara, pa je za α = 240, vp minimalno 6,4 m. Tako je, koristeći rezultat na kraju dela 2.:
pp = 14,38 + 6,4 = 20,78 m. Dalje je, koristeći formule u iz dela 1:
r = (pp/2) / tg(β/2) = 20 410,4 m
h = r * sin(α) = 8301,7 m.
Dakle, ako pretpostavimo da je avion dužine 50 metara, on se na spornoj slici nalazi negde na rastojanju od 14,1 do 20,4 km od posmatrača, i negde na visini od 5,7 do 8,3 kilometara. Po Ayiomamitis-ovoj slici, najverovatnije negde na sredini između tih vrednosti, na visini od oko 7 kilometara.
Ako bi uzeli da je avion kraći, onda bi i ovi rezultati bili manji.
Kolika je greška ove metode? Zavisi od greške pri računanju tačnog prividnog ugla Meseca na nebu koji vidi posmatrač, od grešaka pri merenju odnosa prividnog ugla Meseca i prividnog ugla aviona, i od sitnih zanemarivanja tokom gornjeg računa, ali razmatranje celokupne greške bi bilo vrlo komplikovano i u to se ne bih upuštao.
|
Kliknite na ilustraciju |
 |
|
Slika 41 |
 |
|
Slika 42 |
Deo 4.
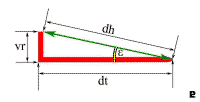
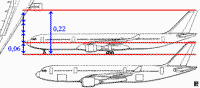
Ako posmatramo sliku 41., zelenu liniju, rastojanje od vrha nosa (pilotske kabine) do vrha repa (vertikalnog stabilizatora) aviona možemo nazvati hipotenuzom aviona i neka je njena dužina dh. Ostale dimenzije na slici 41. su dužina trupa dt i visina repa vr. Ali, vr nije isto što i visina aviona. Visina putničkog aviona koja se daje u referencama je visina od zemlje do vrha repa, kada stoji na zemlji, a tu su uključeni stajni trap i trup, koji uzimaju oko pola ukupne visine, ostala visina je sam rep, a nas interesuje samo hipotenuza. Proverom na više putničkih aviona, ustanovio sam da je visina nosa kod većine aviona na otprilike 1/4 ukupne visine (slika 42.), pa uzeću da je vr 3/4 zvanične visine. Po slici 41. je:
tg (ε) = vr / dt, iz toga sledi da je: ε = arctg(vr/dt),
Kod aviona Airbus 330 (slika 42.), dt = 58,8 m, vr = (3/4)*17,4 m, pa je ε = 12,5 stepeni. Dakle mali ugao. Kod manjih aviona, vrh nosa je na višoj tački u odnosu na ukupnu visinu aviona, recimo negde na oko 30%, i ugao ε bi bio još manji jer bi manje “ostalo” do vrha repa. Samo jako veliki putnički avioni imaju povoljniji odnos za našu hipotenuzu dh sa slike 41., ali čak i kod A380 gde je najveće rastojanje vr, ugao ε je samo 14,6 stepeni.
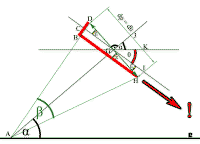
Evo zašto posmatram taj ugao ε. Na slici 43. avion (crvena traka DBH) je postavljen tako da je dh ili zelena duž DH, pod pravim uglom na pravac AG prema posmatraču u tački A, i opet se kao na slici 11. posmatrač i vidni ugao BAH pod kojim on vidi avion nalaze u istoj ravni. Uzeto je da je dh jednako prividnoj dužini dp, da hipotenuza aviona DH čini prečnik vidnog ugla β. Po pravilu uglova sa paralelnim kracima, ugao BHD je jednak uglu CGD, a po pravilu unakrsnih uglova, ugao CGD je jednak uglu HGI, a svi oni su jednaki uglu ε. Kako je ugao HGJ prav ugao, i u njemu važi da je:
α + θ + ε = 900, to je ugao θ između tačaka I, G i K, jednak:
θ = 90 – α – ε.
|
Kliknite na ilustraciju |
 |
|
Slika 43 |
I sad, šta je bitno na slici 43.? Ako je α = 24 stepena, a ε = 12 stepeni, sledi da je θ = 54 stepena, što je jako veliki ugao u odnosu na horizontalu GK u kojoj bi avion normalno leteo. Čak i da je ε = 20 stepeni (što nemamo ni kod jednog putničkog aviona), još uvek bi ugao θ bio veliki, 46 stepeni, što znači da bi avion opasno pikirao ka zemlji! Taj manevar je redak i kod vojnih lovačkih aviona, pa ovde to sigurno nije slučaj. Na slici g. Ayiomamitis-a aviona sa Mesecom, avion nama samo deluje jako nagnut ili baš tako nagnut kao na slici 43., ali nije. Još gore bi bilo da uzmemo da je trup BH (i dalje slika 43.) pod pravim uglom na pravac AG prema posmatraču, tada bi ugao pikiranja θ bio još veći za ugao ε.
Deo 5.
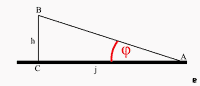
Da proverim još nešto. Po azimutu, Mesec je na jugoistoku, avion ide “u” Mesec i to naniže, dakle deluje da sleće ka jugoistoku, baš prema aerodromu. Po međunarodnom pravilu letenja, putnički avioni se približavaju pistama pod uglom od 3 stepena i pod istim uglom i sleću na nju. Ovaj ugao (posle svih ostalih manevara i zaokreta) avion mora postići najmanje 5-6 kilometara ili 2-3 minuta pred sletanje. Koliko tačno, to zavisi od samog aerodroma. Posmatrajmo pravougli trogao ABD na slici 11. U njemu je:
cos(α) = AB / r, pa je:
AB = r * cos(α)
|
Kliknite na ilustraciju |
 |
|
Slika 51 |
Rastojanje od posmatrača do aerodroma je l = 43 km. Iako je avion bočno od linije posmatrač-aerodrom, radi lakšeg računa uzeću kao da je baš na toj liniji, i kao da se kreće po zemlji, tako da je l zbir rastojanja projektovanih po zemlji od posmatrača do aviona (slika 11., duž AB) i od aviona do aerodroma (slika 51. duž AC ili j):
l = AB + j.
To znači, da avion do aerodroma ima, “po karti”, da pređe još rastojanje j, i to je:
j = l – AB = l – r * cos(α)
Na slici 51., B je tačka u kojoj je avion, a A je tačka u kojoj će avion sleteti. U ovom pravouglom trouglu ACB važi:
tg(φ) = h / j, pa je:
φ = arctg (h / j)
Za slučaj aviona d = 50 m, biće, uzimam u obzir zaključak iz dela 3., i to gori slučaj:
r = 20 410,4 m, h = 8301,7 m, j = 24 354,2 m, φ = 18,8 stepeni.
U boljem slučaju, kada je avion bliže, φ = 10,8 stepeni. Čak i u gorem slučaju, njemu ostaje da se spusti za manje od stepena po kilometru rastojanja, a još sam uzeo rastojanje j koje je nešto kraće od stvarnog. Dakle, on se već polako pripremao za sletanje, bližio se poslednjem uglu od 3 stepena, nema sumnje da bi za preostalih 20-ak kilometara (štrafte j po zemlji) polako postigao krajnji ugao (bez nepotrebnog strmog poniranja).
Deo 6.
Pokušaću da pomoću originalne slike nađem brzinu aviona. Posmatrajmo sliku 61. Pri merenju dužine aviona, uračunao sam i malo, jedva vidljivo ispupčenje na repu trupa. Merenjem pomeraja aviona Δ, našao sam da se on na slici pomerio za 3,3% njegove dužine. Sada nije bitno da li taj pomeraj Δ posmatramo pod uglom ili ne, procenat produženja ostaje isti:
(dpukupno + Δ) = (d + Δ) * sin (α) * sin(δ).
Pa ako je avion dugačak 50 m, znači da se za 125-i deo sekunde pomerio (pravolinijski, u pravcu njegove dužine) za 1,65 m, a to znači da je leteo brzinom (1,65*125*3600) od 743 km/h. Pošto putnički avioni lete brzinom od oko 800 –850 km/h, dakle, i ovo se uklapa, mada upozoravam da je pri ovom merenju dosta velika mogućnost greške.
Dodatak
Dosadašnja analiza je bila vezana neposredno za sliku gospodina Ayiomamitis-a, a sada bih analizirao još par detalja nezavisno od nje.
Deo 7.
Interesovalo me je koliko daleko može avion da odleti pa da se više ne može videti zbog zakrivljenosti Zemlje? Posmatrajmo sliku 71. Na njoj su: rz – poluprečnik Zemlje, rl – poluprečnik putanje leta aviona, i dm – maksimalno rastojanje aviona od posmatrača u tački A do nestanka aviona ispod horizonta u tački B. Na slici 71. važi:
rl2 = rz2 + dm2, a iz ovoga:
Veličina rz je u proseku 6370 km, a rl je samo 10 km veća, pa je dm = 357 km. Dakle, avion koji leti na visini od 10 km mogao bi, teorijski, pomoću nekog optičkog sistema (naravno ne golim okom), bez problema sa atmosferom, konfiguracijom terena i osvetljenošću, da se vidi do 350 km udaljenosti pre nego što zađe ispod horizonta.
Deo 8.
Zanimao me je još jedan detalj. Koliko daleko može da ode avion, a da ga još uvek možemo snimiti? Ako pretpostavimo da ga snimamo fotoaparatom pomoću objektiva od 1000 mm, takav objektiv kod svih proizvođača ima vidni ugao približno od oko 2 stepena po horizontali (2,5 po dijagonali). Pretpostavimo da ga snimimo tako da je toliko daleko da zauzima stoti deo slike po horizontali. Ovo je prilično optimistično za posmatranje (videti stoti deo kadra!), ali još realno za snimanje, jer ako je avion toliko mali na snimku, još uvek će se na fotografiji čija je duža stranica 50 cm, avion videti bar kao neka mrlja širine 5 mm a da se još uvek razlikuje od zrna ili digitalnog šuma.
Posmatrajmo sliku 81. Crno je okvir fotografije, plava crta BC je širina ili dužina aviona (bolje dužina jer onda snimatelj gleda u debeli trup pa još i ima šta da snimi, a ne u tanko krilo), r je rastojanje AE od snimatelja u tački A do aviona BC, a crveni ugao je stoti deo ugla po horizontali snimljene slike. Ovako kako je nacrtano na slici 81., posmatrač gleda u avion tačno pod pravim uglom na širinu krila ili dužinu trupa, pa je dp (prividna dužina) jednaka maksimalnoj dimenziji aviona. U pravouglom trouglu AEB na slici 81. važi:
tg ((2/100)/2) = (dp/2) / r, iz ovoga sledi:
r = (dp/2) / tg ((2/100)/2)
pa je za dp = 50 m, r = 143239,4 m! Dakle, teorijski, orijentaciono, po danu, u najboljem slučaju, po vedrom vremenu i bez problema sa konfiguracijom terena, čak iako snimatelj ne vidi avion ali zna da je “tu negde” u kadru i snima ga pod pravim uglom, mogao bi da ga snimi do daljine od oko 140 km, pomoću teleskopa još i dalje. A posle da ga “lovi” na fotografiji.
|
<< prethodna strana | 1 | 2 | |
|
Literatura: |
- Jelko Kacin: Savremeni avioni i helikopteri / Naša obramba, Ljubljana, 1986.
- Zoran Modli: Piste u noći / Tehnička knjiga, Beograd, 1986
- Logaritamske tablice, 32. izdanje / Školska knjiga, Zagreb, 1984.
- Šema aviona Airbus 330 nađena na Internetu: http://www.aerospaceweb.org/aircraft/jetliner/a330/
- karakteristike dugofokusnih objektiva za Zenit: Zenit 12XP, tehničko uputstvo / Tento, Moskva, 1988-9.
-
karakteristike dugofokusnih Canon
objektiva nađene na Internetu:
http://www.mir.com.my/rb/photography/companies/canon/
fdresources/fdlenses/reflex8002000/2000mm.htm
-
karakteristike dugofokusnih Nikon
objektiva nađene na Internetu:
http://www.mir.com.my/rb/photography/companies/nikon/
nikkoresources/reflex/1000mm.htm

