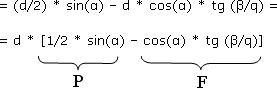|
Prividna veličina aviona
Razmišljajući o tome kako vidimo avion na nebu, palo mi je na pamet da mi zapravo vidimo avion kao njegovu stvarnu veličinu puta neki sinus ili kosinus. Vršeći probe, utvrdio sam da se ipak može nekako naći veličina aviona na nebu. Neće nam trebati baš 3D studio, dovoljna će nam biti obična trigonometrija. Koga mrzi da čita celo izlaganje, rešenja su u pretposlednjim pasusima dela 2. i 3.
Deo 1.
|
Kliknite na ilustraciju |
 |
|
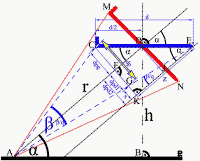
Slika 11 |
Posmatrajmo sliku 11. To bi bio slučaj kada posmatrač u tački A gleda avionu pravo u rep. Slika 11. prikazuje položaje aviona u odnosu na posmatrača, gledano sa bočne strane avoina, pod pravim uglom na liniju leta aviona CE i pod pravim uglom na ravan u kojoj se nalazi ugao CAE između posmatrača i aviona.
U nekoj tački na nebu, u ovom slučaju u tački D na slici 11., avion bi nam izgledao najveći kada bi bio svojim trupom pod uglom od 900 u odnosu na liniju AD koja spaja njega i posmatrača. Dakle, avion bi bio najveći kada je u pitanju “crveni slučaj”, tj. kada avion pikira, kada se obrušava, i tada bi ga videli između tačaka M i N. Ugao pod kojim ga u tom slučaju vidi posmatrač je crveni ugao, ugao između tačaka M, A i N.
U slučaju normalnog leta, to je “plavi slučaj”, što je pod uglom u odnosu na crveni slučaj, avion vidimo “spljošten” i deluje znatno kraći. Ugao pod kojim ga sada vidi posmatrač je plavi ugao, ugao β, između tačaka C, A i E, i vidi se i da je plavi ugao manji od crvenog. U ovom plavom slučaju, avion je iste dužine kao i u crvenom slučaju, neka to bude d, između tačaka C i E, ali posmatrač vidi avion kao da je između tačaka C i G. Ovu novu dužinu aviona nazvaću dp – d prividno, i na slici 11. to je karakteristična žuta linija oivičena plavom bojom. Dakle, žuta linija je ono što posmatrač vidi. Kada se porede crvena i žuta linija, već se nazire koliko avion deluje manji i dalji.
Ovo žuto dp se sastoji iz dpg – d prividno gornje koje se nalazi između tačaka C i F iznad linije AD i normalno na liniju AD, i iz dpd1 – d prividno donje 1 koje se nalazi između tačaka F i G, ispod linije AD. Ovde je ucrtano i rastojanje dpd2 – d prividno donje 2, a to je rastojanje između tačaka F i K, i važi: dpd2 = dpd1+x. Pošto ću pretpostaviti da je tačka D tačno na sredini plavog aviona CE, to su rastojanja CD i DE jednaka i iznose d/2, i time su i pravougli trouglovi CFD i DJE jednaki. Time je i dpd2 = dpg.
Već sa same slike 11. se vidi da je dpd1 nešto kraće od dpg, za rastojanje x između tačaka G i K. Vidi se da ni vidni ugao β nije sasvim simetričan u odnosu na dp, donje parče (ispod duži AD) je nešto manje od gornjeg, i to donje parče ću nazvati ugao β/q. Zbog toga što se radi o malim uglovima, ova razlika u rastojanju i uglu se može zanemariti, ali ipak ću je razmotriti.
Neka je r rastojanje između tačaka A i D. Ovo rastojanje ćemo tražiti kasnije, ali za sada, povucimo ga paralelno nadesno tako da dotiče nos aviona i spaja tačke E i K, što je rastojanje z. Po pravilu unakrsnih uglova, tako dobijamo da je ugao između tačaka G, E i K isto β/q. U pravouglom trouglu GKE važi:
tg (β/q) =x / z, pa je:
x = z * tg (β/q)
Slično ovome, po pravilu uglova sa paralelnim kracima, ugao između tačaka C, E i K i takođe C, D i F je ugao α. U pravouglom trouglu CKE važi:
cos(α) = z/d, pa je:
z = d * cos(α). Dakle,
x = d * cos(α) * tg (β/q).
Dalje, u pravouglom trouglu CFD važi:
sin(α) = dpg / (d/2), pa je:
dpg = (d/2) * sin(α)
Dalje, na liniji FK važi:
dpd1 = dpd2 – x = dpg – x =
Posmatrajmo ova dva člana P i F. Član F je faktor smanjenja prvog člana i time prividne dužine dpd2 prednjeg dela plavog aviona CE sa slike 11. Pošto znamo da je ugao α = 24 stepena (ugao Meseca iznad horizonta u trenutku snimanja), prvi član je konstantan i iznosi P = 0,20336832. Drugi član će se menjati u zavisnosti od toga koliko uzmemo da je q deo ugla β. To može biti polovina, trećina, petina... Već znamo da je β = 3,5 minuta = (3,5/60) stepeni, to je ugao koji zauzima silueta aviona CE, a na slici 11. prečnik te siluete je žuta linija dp. Elem, kad to sve zamenimo, dobija se:
za q = 2, F =
4,65044343 * 10-4
...
za q = 10, F =
9,30088609 * 10-5
Dakle, što je q veće, to je manji uticaj faktora F, i poredeći F sa članom P već za prvo, najmanje q, kada je F najveće, ipak je F još uvek jako malo da bi značajno uticalo na član P. Koliki bi to bio procenat? Evo:
[F(q=2) / P] = 0,0022867 ≈ 0,23%
Dakle, faktor F i time rastojanje x možemo zanemariti i uzeti da je dpd1 = dpg.
Ali, to važi samo za male uglove β. Na slici 11., razlika x je veća, ali je i ugao β znatno veći. Ako je β = 20 stepeni, za q = 2, F = 0,1610827, pa je tada [F(q=2) / P] = 79,2%! Dakle, x bi bilo veliko skoro kao dpd2. Ako je β = 20 stepeni, za q = 10, F = 0,03190171, i tada je [F(q=2) / P] = 15,7%, dakle još uvek bi se malo “osetilo”. Ali pošto je β u našem slučaju malo, neće biti problema.
Dakle, prividna veličina (u ovom slučaju dužina) aviona je:
dp = 2*dpg = 2 * (d/2) * sin(α) = d * sin(α).
|
Kliknite na ilustraciju |
 |
|
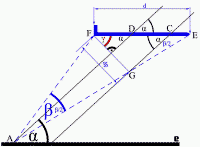
Slika 12 |
Ako se pretpostavi da je dužina aviona 50 m, tada je njegova prividna dužina 20,34 m. Znatno ispod 50m!
Na slici 11., pretpostavljeno je da linija AD prolazi kroz tačku D na sredini plavog aviona CE. Moglo je jednostavnije, da se pretpostavi da je linija AD simetrala ugla β, slika 12. Prema pravilu uglova sa paralelnim kracima, ugao CGE (i dalje slika 12.) jednak je β/2. Kako je ugao β jako mali, to je ugao β/2 još manji u odnosu na prav ugao, ugao CGE se može zanemariti, pa se lako uočava pravougli trougao EGF, u njemu:
cos(γ) = dp / d, i iz toga je:
dp = d * cos(γ) = d * sin(α)
Tako smo dobili isti rezultat kao i na slici 11., ali sam namerno pokazao i prvi način.
E sad, nas zanima koliko je daleko avion? Sada je sve ostalo lako, i ponavlja se analiza iz prethodnih priloga. Pogledajmo opet sliku 11. Treba nam rastojanje AD. Prvo da vidimo koliko je mala dužina FD ispod plavog aviona CE. U trouglu CFD (slika 11.) važi:
cos(α) = FD / (d/2), pa je:
FD = (d/2) * cos(α) = 22,84 m
Zato, zanemariću dužinu FD u odnosu na dužinu AD.
Posmatrajmo pravougli trougao AFC (slika 11.). U njemu je:
tg (β/2) = dpg / r, pa je:
r = dpg / tg (β/2) = [(d/2) * sin(α)] / tg (β/2)
Kada se zameni da je dužina aviona d = 50 m, biće:
r = 19975, 107 m ≈ 20 km.
E sad je već bolje rastojanje do aviona. Zanemario sam dužinu FD u odnosu na celokupno rastojanje r, i stvarno nije neka greška.
Sledeće što nas zanima jeste na kojoj visini je avion na slici? Za tu svrhu, posmatrajmo pravougli trougao ABD (i dalje slika 11.). U njemu je:
sin(α) = h/r, pa je:
h = r * sin(α)
Kada se zameni rastojanje r, u slučaju aviona d = 50 m, biće: h = 8,1246 km. Dakle, imajući u vidu samo ovu dosadašnju analizu položaja aviona, izgleda da je sporni snimak aviona preko Meseca ipak moguć. Ali, ima još.
Deo 2.
|
Kliknite na ilustraciju |
 |
|
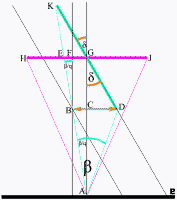
Slika 21 |
Prethodno razmatranje je bilo za avion samo po njegovoj dužini, i kao što se vidi, njegova prividna dužina zavisi od ugla između površine Zemlje (tangente u tački A, slika 11.) i pravca (AD) između posmatrača i aviona. Ako posmatramo avion samo po širini, slika 21., tu će nam biti važan ugao između pravca AG ka avionu i ose aviona HJ ili KD, tj. slika prikazuje slučaj kada posmatrač gleda avion pod pravim uglom u odnosu na raspon krila (ili dužinu trupa), i prikazuje pogled odgore, tako da su posmatrač i avion u istoj ravni.
Kao i na slici 11., i ovde imamo 2 slučaja: prvi slučaj je ružičasti avion između tačaka HJ koji se nalazi tačno pod 90 stepeni u odnosu na pravac AG između posmatrača i aviona. Drugi slučaj je tirkizni avion KD čija je osa pod uglom δ u odnosu na pravac AG prema posmatraču. Taj avion KD zauzima ugao β od vidnog polja. Prividna širina tirkiznog aviona za posmatrača je narandžasta duž BD i BD je znatno kraća od duži HJ što je slučaj kad bi posmatrač video avion u punoj širini.
Kolika je duž BD? Usvojićemo da je duž GD = d/2, tj. pola širine aviona (kao što je bila i duž CD na slici 11.). U pravouglom trouglu DCG (slika 21.) važi:
sin(δ) = CD / (d/2), pa je:
CD = (d/2) * sin(δ)
Da se opet ne zamaramo traženjem tačne dužine duži BC, ako pretpostavimo da se β jednako deli sa obe strane, sa slike 21. je jasno da će BC biti najviše jednaka duži CD ili kraća od nje. To znači da će i prividna veličina BD, tirkiznog aviona KD čija je osa pod uglom δ, za posmatrača biti najviše:
dp = 2*CD = d * sin(δ).
I sada, ako bi avion širine d = 50 m bio svojim trupom pod uglom od 45 stepeni u odnosu na posmatrača (što je slučaj tirkiznog aviona KD na slici 21., a deluje i da je pod tim uglom i avion na originalnoj Ayiomamitis-ovoj slici), njegova prividna veličina će za posmatrača biti 35,36 m. Eto opet značajnog skraćenja siluete. Pa sad, ako opet uzmemo onaj “legendarni” tangens (trougao ACD na slici 21.):
tg (β/2) = CD / AC,
a AC je rastojanje r od posmatrača do aviona (zanemarujući duž CG u odnosu na r, kao i delu 1.), tada je:
r = CD / tg (β/2).
Kako je CD = 35,36/2 m, a β=3,5 minuta, to je r = 34726,5 m. Opet dobijamo bliže rastojanje do aviona (manje od 50 km).
A na kolikoj visini je avion? On je na visini (koristi se formula sa slike 11.):
h = r * sin(α)
što daje 14124,5 m. Ovo je velika visina, ali ipak bliža visini leta. (Mada je Konkord mogao da leti i do 15600 m, ne mogu drugi putnički avioni pa nećemo 14 km uzimati u obzir.) Verovatno mi je greška u pretpostavljenom uglu δ. Ako je on 30 stepeni, prividna veličina (u ovom slučaju širina) aviona BD je 25 m, rastojanje do aviona je 24555,3 m, a nalazi se na visini od 9987,6 m. Dakle, 30 stepeni bi možda mogao da bude pravi ugao pod kojim se vidi avion razmatrajući njegovu prividnu veličinu samo po širini. Iz ličnog iskustva znam da ponekad na ravnom teško uočim razliku između ugla od 30 i kojeg stepena i 45 stepeni, a na slici koju razmatramo je taj ugao u tri dimenzije tako da ga nije baš lako oceniti. Na slici 61. avion je zarotiran za 50 stepeni, kao prema posmatraču, kao prema liniji AG na slici 21., ali se uočavaju deformacije na trupu, avion nije potpuno prav, tako da ni taj nađeni ugao nije realan ugao, a moguća greška u odnosu na prav ugao koji sam hteo da postignem je do 2 stepena.
|
Kliknite na ilustraciju |
 |
|
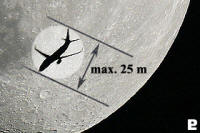
Slika 22 |
U oba slučaja, i pri razmatranju po dužini i pri razmatranju po širini, zaključak je da ne treba uzeti preterano veliku prividnu dimenziju aviona. Ako se uzme do 20 – 25 metara (slika 22.) dobijaju se realni rezlutati. A slike 11. i 21. pokazuju da kad se avion posmatra pod uglom da su zaista moguća značajna odstupanja od njegovih stvarnih dimenzija.
Da stvar bude veća, ukupna prividna dimenzija aviona je kombinacija ove dve, kombinacija skraćenja po dužini i skraćenja po širini, pa je zapravo:
dpukupno = d * sin (α) * sin(δ).
I sad, ako uzmemo d = 50 m, α = 240, i (opet) δ = 450, sledi: dpukupno = 14,38 m, r = 14124,5 m, i h = 5745 m. E, ovo su još realniji rezultati blizu snimatelja i blizu aerodroma. Ali, ni to nije sve.
| 1
|
2 |
sledeća strana >>