|
05. 02. 2007.
U jednom od blogova sam napisao da je brzina šatla u orbiti između 27.360 i 28.970 km/h. Ono što tom prilikom nisam rekao jeste da se taj raspon brzina ne odnosi na svaku letilicu koja je u orbiti, već samo na određene, koje se oko naše planete kreću na isti način. Odmah treba reći da su brzine u orbiti oko Zemlje različite za različita tela odn. letilice, što zavisi od mnogih fakrora: visine, težine, perioda rotiranja itd.
Kao i uvek, vrlo je bitno prethodno razjasniti eventualne nejasnoće u terminologiji. Reč "orbita" predstavlja putanju kojom se kreće neko telo pod uticajem sile gravitacije. U tom kontekstu, orbitu najčešće zamišljamo kao putanju nekog nebeskog tela ili vasionskog broda oko drugog tela, koje stručno nazivamo primarnim telom. Naprimer, telekomunikacioni sateliti prate orbitnu putanju oko Zemlje, dok Zemlja prati svoju orbitu oko Sunca. Ono opet prati svoju putanju oko jezgra galaksije, a izgleda da i ona prati neke svoje staze ... i tako ko zna dokle. Proučavanje kretanja veštačkih satelita i svemirskih letilica pod uticajem sila kao što je gravitacija spada u domen interesovanja tzv. orbitne mehanike. U toj nauci ima jedna jednačina koja predstavlja srž čitave naše priče – to je ona koja opisuje Njutnov drugi zakon kretanja. Taj zakon kaže da ako silom (F) utičemo na neki objekat mase (m), doćiće do ubrzanja (a). Napišimo to ovako:
Još jedna ključna jednačina koju nam je Njutn ostavio u amanet je njegov Univerzalni zakon gravitacije. On kaže: Dva tela mase M i m i udaljena r, privlače jedno drugo jednakom i suprotnom silom u pravcu linije koja spaja središta ta dva objekta. Jačina te sile iznosi:
Vidimo da se ovde javlja još jedna nepoznata zvana G, ili univerzalna gravitaciona konstanta. Ona opisuje uzajamno privlačenje dva tela različite mase i jednaka je:
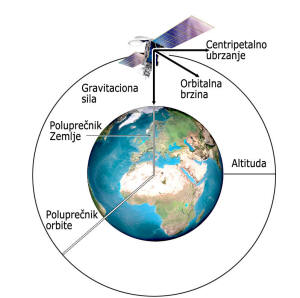
Najprostiji slučaj u orbitnoj mehanici zove se jednakoubrzano kružno kretanje. Drugim rečima, takva orbita je prosta kružnica, sa konstantnim poluprečnikom oko primarnog tela, i po njoj se telo kreće konstantnom brzinom. Razlog za takvu konstantnu brzinu leži u činjenici da orbitirajući objekat, krećući se pravom linijom, neprestano ubrzava ka središtu primarnog tela. Duž putanje ne postoji linearno ubrzanje, već samo ubrzanje u pravcu kretanja. Takvo ubrzanje nazivamo centripetalnim, jer je pravac kretanja uvek ka unutra, prema centru kružne orbite. Ovo ubrzanje (a) može se izračunati ako se zna linearna brzina objekta po orbiti (v) i poluprečnik te orbite (r).
Unevši ovu jednačinu ubrzanja u jednačinu Njutnovog drugog zakona, dobićemo izraz koji definiše jednakoubrzano kružno kretanje:
Ako napravimo jednakost sa Njutnovim univerzalnim zakonom gravitacije, odatle možemo izraziti kružnu brzinu:
Pada u oči jednostavnost ove jednačine. Ona kaže da je brzina nekog tela po kružnoj orbiti proporcionalna jedino masi primarnog tela, a obrnuto proporcionalna poluprečniku kružne orbite. Pošto je u našem slučaju primarno telo Zemlja, a telo u orbiti spejs šatl, odredićemo pomoću navedene jednačine brzinu šatla u orbiti:
Da bi učinili jednačinu malo prijemčljivijom, označićemo masu M kao masu Zemlje (MZ), a poluprečnik orbite kao poluprečnik Zemlje (RE) plus visina šatla iznad površine (h).
gde je MZ= 5,98 × 1024 kg, RZ = 6,378 × 106 m. Jedino što još ne znamo jeste visina na kojoj šatlovi lete. Ona zavisi od vrste misije na kojoj se ove letilice nalaze. One koje su vezane za Hablov teleskop (HST) ili Međunarodnu svemirsku stanicu (ISS) zahtevaju visine i do 400 km [1]. Ali, najtipičnije visine se za šatlove kreću tu negde oko 300 km. Ako unesemo datu visinu u jednačinu za brzinu na kružnoj orbiti, dobićemo da iznosi oko 7.730 m/s ili 27.830 km/h.
Na ovaj način smo otprilike dobili brzinu koju smo i očekivali, jer tipična brzina šatlova oko Zemlje iznosi oko 28.165 km. Međutim, nismo rekli da šatlova orbita u stvarnosti nije savržena kružnica, već elipsa. Ipak, bilo kako bilo, jednačine sa kojima smo radili dale su nam prilično dobru aproksimaciju tipične brzine šatlova u orbiti. Iste ove odnose možemo primeniti i na bilo koja druga tela u orbiti. Naprimer, postoji jedna posebna vrsta orbita, poznata kao geostacionarna ili geosinhrona orbita, koja se često skraćeno piše kao GEO [2]. Svaki satelit na takvoj orbiti obiđe Zemlju za tačno 24 sata, tako da izgleda kao da je satelit sve vreme stacioniran [3] iznad jedne iste tačke na Zemlji. Takav tip orbite je veoma pogodan za mnoge vrste komunikacionih, meteoroloških ali i vojnih i obaveštajnih satelita. Kružna geostacionarna orbita u ravni Zemljinog ekvatora nalazi se na visini od tačno 35.786 km, što zahteva brzinu rotacije od 11.068 km/h. Istu jednačinu možemo primeniti i na orbitu Zemlje oko Sunca. Ni ta orbita nije neki perfektan krug, ali dovoljno da dâ dobru procenu orbitne brzine naše planete. U ovom slučaju, vrednost M postaje masa Sunca (MS) a poluprečnik orbite prosečno rastojanje Sunce/Zemlja (RZemljine orbite). MS = 1,99 × 1030 kg, RZemljine orbite = 1,4959 × 1011 m. Primenivši našu jednačinu za brzinu u kružnoj orbiti i uvrstivši ove vrednosti, dobićemo prosečnu brzinu od 29,783 m/s. Drugim rečima, naša malešna planeta juri oko Sunca zapanjujućom brzinom od oko 107.219 km/h i po svojoj orbiti svake godine stigne da prevali 924.375.700 km, što je jednako 6,179 A. J.! Nadam se da ste pritegli sigurnosne pojaseve!
(22.02.2007.)
|
SHUTTLE NA POPRAVNOM ILI U MIROVINU!? MINUTE STRAHA ZA ASTRONAUTE (Space shuttle 2006) Spejs šatl Kolumbija eksplodirao Da li je posada Kolumbije mogla biti spasena? Da li bi se posada Burana spasla?
|