10. novembar 2008. Jeste li pogledali ikad nulu u oči, te velike okrugle oči, i zapitali se da li se u toj praznini ipak nešto krije? Ko je nuli dao ime, smisao, sadržaj, suštinu, mesto na brojnoj osi? Piše: Milica Tomić

Nula. Zovu je i Ništica. Ili Praznina. Nepostojanje. Ali, kako je ona uopšte dospela među ostale brojeve koji, za razliku od nje, prebrajaju nešto što postoji? Priča o prihvatanju i odbacivanju, poznavanju i nepoznavanju nule, praznine i beskonačnosti seže duboko u istoriju, prati razvoj matematike i u mnogome se dotiče filozofije različitih naroda u drevnoj i novoj istoriji.

Zanimljivo je da je baš Vavilon, čije su kule danas u nekim krugovima simbol težnji da se približimo Bogu na loš način, (neko bi rekao i simbol „urušavanja svih čovečanskih kula kojima smo mislili da smo prišli Bogu u moći, pa verovatno ga i prestigli“), iznedrio jednu tako moćnu stvar koja vekovima obara velike naučne teorije, a i dan danas nas ostavlja nemoćnim pred pitanjima praznine, stvaranja, nestanka.

Primitivna nula se, dakle, prvi put pojavila u starom Vavilonu (gde je način obeležavanja brojeva bio potpuno drugačiji od onih načina koje poznajemo danas, a i Vavilonci su koristili seksagezimalni sistem zasnovan na broju 60, umesto našeg današnjeg decimalnog sistema zasnovanog na broju 10), ali samo kao vrsta pokazivača mesta u brojevima, što je bilo veoma napredno jer je omogućilo mnogo lakše računanje.

Vavilonska tablica sa brojevima

U IV veku pre nove ere Aleksandar Veliki je prilikom osvajanja Istoka preneo tu vavilonsku nulu pokazivača u Indiju. Nula je u Indiji dobila brojnu vrednost i mesto na osi. Bila je velika stvar da nešto što broji ništa, nešto bez količine postane broj. Stari indijski matematičari su se usudili i da dele nulom utvrdivši da kada se doda ili oduzima bilo šta od razlomka 1/0, ništa se ne dešava jer je broj 1/0 (a to je, zapravo, jednako beskonačno) nepromenljiv. Posle VII veka, u prodoru Islama na daleki Istok, Arapi su saznali za indijske brojeve, pa se njihova matematika razvijala uz nulu.

Italiji i zapadnom svetu nulu je u XIII veku predstavio matematičar Leonardo Pizano – Fibonači, ali bez mnogo uspeha. Njegov je otac bio trgovac, pa je Leonardo putovao u Afriku gde se školovao u arapskim školama. Po povratku u Italiju napisao je više knjiga o matematici u kojima je između ostalog prikazao prednosti arapskih brojeva i nule. Zbog lakog računanja, nove brojeve su prvi prihvatili trgovci mada ih je država zabranila zbog mogućnosti lakog falsifikovanja.

Lagani prilazak nuli

U XVII veku francuski matematičar i filozof Rene Dekart načinio je koordinatni sistem koji se danas koristi, sa tim izuzetkom što nije uzeo u obzir negativne brojeve. Ali uveo je nulu. U tako lepom koordinatnom sistemu uvideo je vezu između oblika i jednačina i time zasnovao analitičku geometriju.

Nula je i dalje bila bezdan bez adekvatnog obrazloženja zbog neprijatnosti do kojih dovodi deljenje njome. Iako ni ser Isak Njutn nije razumeo šta predstavlja razlomak sa nulom u imeniocu, on ga je legalizovao preko diferencijalnog računa. Mnogi su u takav račun sumnjali, ali rezultati su bili nesumnjivo ispravni. U osnovi diferencijalnog računa je, u stvari, deljenje dve veoma male veličine, toliko male da tek što nisu nule. Činjenica da nisu nule nego brojevi vrlo bliski njoj, ali ravnopravni kao svi drugi, upravo održava ovaj račun mogućim.

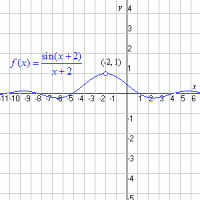Granična vrednost funkcije

Njegov je značaj i dubina daleko veća od običnog deljenja. Zakoni fizike koji su do tada bili pisani običnim jednačinama mogli su sada biti predstavljeni jednačinama u diferencijalnom obliku, čime je dobijena veća opštost. Danas su ovakve jednačine oruđe bez kojeg se ne ulazi u rešavanje ozbiljnih problema u fizici i svim drugim naukama i oblastima koje koriste matematiku.

Zbog svoje sumnjivosti, diferencijalni račun je počeo više da se koristi tek krajem XVIII veka, dok su se matematičari sve više motali oko nule uz pomoć redova, konvergentnih funkcija, a konačno joj uz pomoć graničnih vrednosti prišli najbliže. Ali, kako se to u matematici kaže, nuli se prilazi tek u beskonačnosti.

Nedodirljiva je

Zašto nam ona i njena sitna struktura stalno izmiču? Može li se nula obuhvatiti više od ovoga? Može li se nekako ući u samu nulu kad smo joj već toliko matematički prišli? Šta to znači da se do nule dolazi tek u beskonačnosti?

Otkrivanje odgovora na ovakva pitanja daće nam nauka koja je u svom svetu pronašla primenjenu nulu. To je svet moderne fizike.

Ovaj broj je zavrteo fizičarima mozak i naveo ih da se dovijaju na sve dozvoljene, a još više na do tada nedozvoljene načine ne bi li ga dokučili. Ne bi li ga pobedili.

Istorijski prva revolucionarna nula otkrivena u prirodi jeste apsolutna nula temperature ili nula stepeni na Kelvinovoj skali. To je najniža moguća temperatura. Nema ništa hladnije od nje, ali može li se i ona dostići?

 

BIOGRAFIJA OPASNIH IDEJA Čitava istorija padova i proboja ovog broja i njegovi problemi lepo su objašnjeni u knjizi Nula: biografija opasnih ideja. Njen autor, magistar matematike Čarls Sife je profesor žurnalistike na Njujorškom univerzitetu i novinar magazina Science. Članke takođe piše za časopise New Scientist, Scientific American, The Economist, Science, Wired UK, The Sciences. Autor je više vrlo zanimljivih knjiga iz popularne nauke.

Kao i u matematici, i u prirodi se pokazalo da je nula samo nekakva vrsta imaginacije. Apsolutna nula je nedodirljiva. Ne može se dostići. Ona je samo granična vrednost kojoj se možemo približiti, ali joj ne možemo potpuno prići. To bi bilo stanje u kojem bi predmet koji želimo da ohladimo izgubio svu svoju energiju, a u stvarnosti to nije moguće.

Uzmimo jednu bananu kao predmet koji želimo da ohladimo. Moraćemo da je stavimo u kutiju i zamrznemo. Ali ako kutija nije na asolutnoj nuli, ona poseduje atome koji vibriraju (što znači da su na određenoj temperaturi, to jest da poseduju određenu energiju), a njihove vibracije pokreću atome banane da i oni vibriraju, te naša banana, ipak, ima izvesnu temperaturu. Čak i kada bi lebdela u potpunom vakuumu, ne dodirujući ni jednu česticu, njene atome bi na vibriranje naterali fotoni svetlosti koju zrači kutija. (U modernoj fizici sve što se kreće ili vibrira, mora i da zrači.) Dakle, pošto je ne možemo potpuno izolovati od okoline, banana uvek mora imati neku temperaturu. 

Nula je varljiva

Od apsolutne nule je krenula da se razvija termodinamika, pa zatim statistička fizika, da bi se na kraju došlo do kvantne mehanike. E, u njoj već ima previše čudnih stvari, a od najčudnijih je relacija neodređenosti Vernera Hajzenberga. Ona nam tek otkriva koliko ne znamo, tačnije koliko ne možemo ni znati o ovom svetu. Ali i ona sama takva kakva je – neodređena, fizičarima mnogo znači.

Recimo da znamo tačno gde se nalazi predmet za koji želimo da saznamo koliku ima energiju. (U pitanju je tačnost koja se meri veličinama mnogo manjim od milimetra i mikrometra. Čak nam ni najbolji mikroskop ovde ne može pomoći. To se prosto ne vidi. Samim tim, da bi dimenzije bile u skladu, uzmimo za predmet koji razmatramo česticu.) Hajzenbergova relacija kaže da ako možemo tačno da lociramo predmet (česticu), mi onda nikako ne možemo znati njegovu energiju. Sami smo sebi napravili problem jer smo merenjem položaja našim sitnim lenjirom morali doći u kontakt sa česticom i promeniti joj energiju, te više ne znamo koja je energija njena, a koja je dodata samim činom merenja! Što bliže odredimo položaj čestice, mi, u stvari, sve manje znamo o njenoj energiji.

Prostor-vreme

Važi i obrnuto. Ako znamo energiju čestice, mi nemamo pojma gde se ona nalazi. Ne znamo koja je to čestica, to jest čija je to zapravo energija. Zvuči paradoksalno, ali u fizici je čak i to od pomoći.

Još jedan problem koji nula pravi u kvantnoj mehanici su nula-dimenzione čestice, a takvi su elektroni (i ostali leptoni) ali i kvarkovi. Njihova nedimenzionalnost čini da mi uopšte ne znamo kolika je masa i naelektrisanje na primer elektrona. Ako bismo se približili beskonačno blizu čestici-tački, izmerili bismo beskonačnu masu i isto takvo naelektrisanje. Masa i naelektrisanje elektrona koje nalazimo u tablicama iz fizike su zapravo utvrđene na određenoj razdaljini od čestice. Na nultoj razdaljini imamo problem.

Kad nula ima silu

Razmotrimo sada vakuum. On ima gustinu jednaku nuli; to je, u stvari, prazan prostor. Ispostavilo se da priroda na neki svoj način ne voli prazan prostor. Holandski fizičar Hendrik B. G. Kazimir je ustanovio da postoji vrlo slaba sila koja deluje u vakuumu, a prouzrokovana je pritiskom čestica koje nastaju i nestaju sa svih strana (opet jedna od kvantnih zanimljivosti), ali ne mogu ući u kutiju sa vakuumom. U kutiju određenih dimenzija mogu ući samo čestice izvesnih energija, nikako svih energija (još jedno od čuda kvantne teorije).

Stidljiva

Nule postoje i u Univerzumu. Razbacane su unaokolo, a zovemo ih crne rupe. Crna rupa je tačka u svemiru koja ima ogromnu, zapravo beskonačnu masu. Kao takva, ona privlači objekte ogromnom gravitacionom silom, ali nije to jedina njena osobina. Ono što je zanimljivo u vezi s njom je da ona zakrivljuje prostor-vreme do beskonačnosti, te, u stvari, pravi rupu u našem divnom glatko-krivudavom prostor-vremenu. Dakle, svemir ne samo što je iskrivljen, krivudav, već ima i izvesne nule, rupe u sebi!

Međutim, nula (singularitet) u crnoj rupi je zaštićena od posmatrača. U nju bi mogao svako da upadne, ali niko ne može direktno da je gleda jer njena jaka gravitaciona sila ne dozvoljava ničemu što bismo mi mogli videti da napusti rupu. Postoji takozvani horizont događaja iza kojeg informacije ne izlaze. Kao da priroda hoće da sakrije te sramotne rupe.

Stomačić prepun tajni

Teorija struna - umetnički prikaz

Ima rešenja i za nulu. Pošto je fizika jedna domišljata i filozofski nastrojena nauka, ona je dozvolila postojanje teorije iz koje je nula izbačena (barem po pitanju dimenzija). To je teorija struna. U njoj čestice više nisu tačke bez dimenzija, nego su jednodimenzione. Na taj način pomenuti problem sa nultom razdaljinom i beskonačnim veličinama za masu i naelektrisanje nestaje.

No, ova teorija se smatra više filozofijom nego naukom. Ona se ne može dokazati pošto joj se, po svemu sudeći, ni blizu ne može prići eksperimentom. Ona kao da postoji samo u vidu matematičkog objašnjenja prirode.

Pomalo kao i nula. Kada je pišemo na papiru, uokvirujemo jednu prazninu. Indijci su uveli takvu oznaku uokvirivši ništa jer je ono bilo jedini sadržaj nule.

Danas nam se čini da je ona u tom svom trbuhu sakrila mnoge tajne prirode. Oči današnje nauke ne mogu je razotkriti.

NULTA GODINA Nula na početku nove ere uvela bi mnogo olakšica u računanje vremena kojih mi danas nismo ni svesni. Mi smo programirani na kalendar bez nule. Na kraju 1999. godine bilo je sasvim logično sa novom godinom dočekati i novi milenijum, a da svetski kalendar ima godinu sa oznakom 0, ne bi bilo potrebno objašnjavati zašto XXI vek počinje 2001. godine, a ne 2000. Između prve godine pre nove ere i prve godine nove ere bila bi nulta godina i kalendar bi bio pregledniji. Ni beba kad se rodi nema jednu godinu, nego je napuni prilikom prvog rođendana.

 

Komentari na sajtu B92 o ovom članku Postojeći komentari

Pošaljite svoj komentar na B92 Pošaljite komentar

 

Izvor: http://www.b92.net/zivot/nauka.php?nav_id=327814