Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5

Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA

---

4. Metod amplituda-magnituda

Metodi poznati pod nazivom metodi amplituda-magnituda razvijeni su u cilju modeliranja oblika asteroida, što metodi epohe nisu mogli da pruže. Ovakvi metodi se najbolje uklapaju u klasičnu predstavu o modeliranju oblika. Za razliku od metoda epohe, metod amplituda-magnituda izvlači informacije o obliku na osnovu oblika krive sjaja; geometrija posmatranja uzima se u obzir samo u tom smislu da se osobine krive sjaja prouzrokovane menjanjem geometrije posmatranja odvajaju od osobina prouzrokovanih oblikom.

Prve upotrebljive varijante ovog metoda dali su Zapala (Zappala, 1981; prema: Magnusson, 1989) i Magnuson (Magnusson, 1986). Do kraja osamdesetih godina data su još neka poboljšanja (npr. Pospieszalska-Surdej, Surdej, 1985; Magnusson, 1989) koje ipak nisu unela ništa suštinski novo. Tek devedesetih godina, radovima Kvaitkovskog (Kwaitkowski, 1994), kao i Magnusona i Eriksona (Magnusson, Erikson, 1993), koji su doneli novi pristup i kombinovanje sa elementima metoda epohe, ostvaren je novi prodor u ovoj oblasti.

Metod amplitude-magnitude podrazumeva nešto više aproksimacija nego prethodni metod; u pitanju su sledeće pretpostavke:

-          površina asteroida odbija svetlost po Lomel-Zeligerovom zakonu

-          ne postoje varijacije albeda na površini

-          ne postoji precesija pri kretanju asteroida

-          astreroid ima oblik troosnog elipsoida

Kao što se vidi, poslednja pretpostavka je najspekulativnija i praktično nikad ne može biti ispunjena, što predstavlja i najveće ograničenje ovog metoda. Međutim, teorijska istraživanja su pokazala (npr. Chandrasekhar, 1969; Kaulla, 1996) da kod prečnika (u smislu srednje dimenzije) većih od oko 300 km čak i odstupanja od sfernog oblika nisu velika, a da za objekte prečnika većeg od 10-50 km troosni elipsoid predstavlja sasvim dobru aproksimaciju. U svakom slučaju, ovaj metod daje tzv. fotometrijski model asteroida, koji predstavlja najbolju aproksimaciju realnog oblika oblikom elipsoida.

Kao što je rečeno, klasični metodi amplitude-magnitude koriste Lomel-Zeligerov zakon (ili Hapke-Irvinov), koji predstavlja razumnu aproksimaciju u većini slučajeva. Kasnije će biti spomenute neke novije varijante ovog metoda koje koriste neke druge zakone odbijanja (Hapkeov ili Lume-Bauelov). Osnovna ideja metoda sastoji se iz činjenice da je, ako se usvoje pomenute aproksimacije, ukupna osvetljenost površine asteroida proporcionalna vidljivom poprečnom preseku, uz eventualne korekcije vezane za tzv. okultacioni efekat i negeometrijsko odbijanje svetlosti.

Asteroid je u narednim razmatranjima predstavljen troosnim elpsoidom  pri čemu je . Rotacija se vrši oko - ose. Oznake ekliptičkih koordinata asteroida i severnog pola ostaju neizmenjene. Važno je napomenuti da se kod ovog metoda smer rotacije ne može odrediti, pa se pod “severnim polom” podrazumeva severni pol u smislu pravila desnog zavrtnja, tj. u slučaju retrogradne rotacije on će se nalaziti na južnoj hemisferi.

Sa  će ubuduće biti obeležen ugao rotacije (tj. ugao između pravca asteroid-Zemlja i početnog pravca najveće poluose). Kao što je uobičajeno, fazni ugao je označen sa . Za naredna razmatranja neophodna su još dva ugla: tzv. nagibni ugao (eng. aspect angle) i iskošenje (eng. obliquity). Nagibni ugao (označen sa ) predstavlja ugao između ose rotacije asteroida i pravca asteroid Zemlja, dok iskošenje (označeno sa ) predstavlja ugao između ose rotacije i prave koja prolazi kroz centar asteroida i normalna je na ravan asteroid-Zemlja-Sunce

Veza nagibnog ugla i ekliptičkih koordinata asteroida (koje se sa velikom tačnošću mogu izračunati) dobija se primenom kosinusne teoreme:

    (23)

Elementarnom primenom linearne algebre (vidi Dodatak 2) može se pokazati da projekcija poprečnog preseka asteroida u opoziciji iznosi:

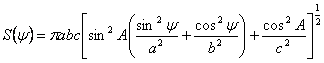    (24)

Ako se početna orijentacija izabere tako da za  najmanja poluosa posmatranog asteroida bude okrenuta u pravcu - ose, tada će najmanja i najveća vrednost projekcije iznositi:

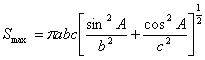    (25)

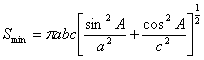    (26)

Iz navedenih jednačina sledi izraz za amplitudu u opoziciji (npr. Magnusson, 1986):

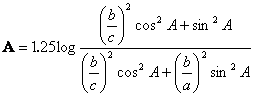    (27)

Kada se nagibni ugao u (27) izrazi iz (23), dobija se jednačina po , ,  i . Za dobijanje ovih parametara potrebne su krive sjaja iz četiri različite opozicije. Kao što se vidi, potrebno je manje podataka nego kod metoda epohe. U pojedinim slučajevima je dovoljno i manje krivih, s obzirom na veoma izraženu zavisnost kvaliteta rešenja od parametra . Ipak, moguće su i suprotne situacije (npr. u slučaju da sve korišćene

 opozicije imaju slične geometrije posmatranja). U ovim slučajevima potrebno je još krivih sjaja; u njihovom nedostatku, može se, umesto direktnog rešavanja, primeniti “skeniranje” celog neba po koordinatama pola, i zatim izdvojiti rešenje sa najmanjim  odstupanjem. Takođe je moguće i fiksiranje i potom variranje jednog od odnosa osa; konačno, asteroid se može aproksimirati obrtnim elipsoidom i tako eliminisati parametar , koji je, kako se u praksi pokazalo, najproblematičniji i često se ne može

 odrediti čak ni u slučaju kvalitetnih posmatračkih podataka.

Drugi pristup, uveden prvi put 1985.godine (Pospieszalska-Surdej, Surdej, 1985), umesto uvođenja direktne zavisnosti od amplitude, koristi zavisnost između osvetljenosti i ugla rotacije. Naime, ako se uvede relativna osvetljenost tačke na krivoj u odnosu na minimalnu osvetljenost :

    (28)

jednačina (15) postaje:

    (29)

pri čemu je:

    (30)

Zamenom nagibnog ugla iz (23) ponovo se dobija jednačina sa polarnom orijentacijom i odnosima osa kao nepoznatim parametrima. Vrednost veličine  se dobija kao nagib funkcije , pri čemu  varira u intervalu , a osvetljenost svake tačke na krivoj se dobija iz njene magnitude. Dakle, ovaj postupak koristi sve tačke krive, a ne samo ekstreme. Sama procedura računanja parametara modela ne koristi jednačinu (30), koja je nepogodna za numeričke proračune. Ako se kosinus nagibnog ugla izrazi iz (30) i ubaci u (23), dobija se:

    (31)

I u ovom slučaju važe opšte napomene o broju korišćenih krivih. Naravno, različitim kombinacijama znaka poslednjeg člana za različite krive, dobija se veliki broj različitih sistema, ali se u praksi pokazalo da samo jedna ili, ređe, nekoliko, kombinacija daje sistem koji ima rešenja.

Važna mana opisanih metoda jeste izvesna neprilagođenost neopozicionim posmatranjima, s obzirom da navedene relacije između amplitude i geometrije posmatranja važe samo za slučaj geometrijskog odbijanja svetlosti i osvetljenosti cele vidljive projekcije. Ovaj problem je dugo ostao nerešen, i tek pojavom sasvim novih tehnika (v. sledeći odeljak) on je zadovoljavajuće rešen. U Zapalinom i Magnusonovom pristupu, ovaj problem se rešava uvođenjem linearne zavisnosti između amplitude u proizvoljnoj geometriji posmatranja i amplitude u opoziciji, za koju se pretpostavlja da je poznata (a za većinu asteroida i jeste precizno određena). Ovu zavisnost proučavali su Zapala i saradnici (Zappala et al, 1990). Raspoloživi prostor i namena članka ne omogućavaju duže zadržavanje na ovoj zavisnosti; dovoljno je reći da se koeficijent pravca ove zavisnosti određuje takođe iz što većeg broja posmatranja i da se može naći u većini fotometrijskih kataloga asteroida. Ipak, postoje slučajevi u kojima se ova zavisnost, koja je i inače slabo teorijski zasnovana, ne može primeniti.

Drugi opisani pristup omogućava nalaženje semianalitičkog rešenja ovog problema. Kako je pokazano u Dodatku 2, leva strana izraza (24) za površinu se za proizvoljnu geometriju posmatranja zamenjuje sa:

    (32)

Funkcija  ima komplikovan oblik, naveden u Dodatku 2, koji je veoma nepovoljan za praktične proračune, pa se ova varijanta obično i ne koristi kod neopozicionih posmatranja. Inače, izraz (32) uključuje samo tzv. okultacioni efekat (tj. činjenicu da je deo projekcije neosvetljen). Geometrijsko odbijanje svetlosti leži u osnovi ovog postupka i negeometrijsko odbijanje se ne može uzeti u obzir.

Metod amplitude-magnitude je dugo vremena bio najrasprostranjeniji metod za modeliranje asteroida. On pruža mogućnost preciznog određivanja polarne orijentacije i, u zavisnosti od kvaliteta posmatračkih podataka, daje manje ili više dobru aproksimaciju oblika. Dva koncepta koji su se nametnuli kao najbolje tradicionalne varijante su Magnusonov i Sardijev, koji su izloženi detaljno. Sardijev pristup je pogodniji jer ne uključuje same vrednosti amplituda, čime se izbegava nesigurno kombinovanje amplituda različitih posmatranja; osim toga, on direktno pruža uvid u adekvatnost elipsoidne aproksimacije (jer u slučaju izrazito neelipsoidnog oblika ne postoji linearna zavisnost osvetljenosti od ugla rotacije). Sa druge strane, on uvećava grešku, koja u blizini maksimuma postaje najveća (zbog pretvaranja u osvetljenost) i ne može se iskoristiti za neopoziciona posmatranja.

Treba reći da postoje i metodi koji direktno uključuju i magnitudu i koji pružaju čak i apsolutne dimenzije asteroida (npr. Surdej et al, 1986), ali koji su veoma nesigurni, zbog čega se u praksi i ne koriste, pa nisu ovde opisani.

vrh