|
|
Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5
- Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA
3. Metod epohe
Najstariji metod za modeliranje asteroida, razvijen još krajem sedamdesetih godina, a poboljšan tokom osamdesetih, poznat kao metod epohe, predstavlja pokušaj da se iz krivih sjaja dobije što više informacija uz korišćenje što manjeg broja početnih pretpostavki, uz očuvanje jednostavnosti. Posle Tejlorovog rada (Taylor, 1973), objavljeno je nekoliko poboljšanja ovog metoda (Taylor, Tancredi, 1983; Michalowski, 1988; Drummond et al, 1988); malobrojni noviji radovi na ovu temu (npr. Michalowski, 1993) ne donose nikakva značajnija poboljšanja. Posle toga, ovaj metod je uglavnom potisnut, i našao je svoje mesto tek u kombinaciji sa metodima amplituda-magnituda (v. odeljak 5). Mada daje samo sinodički period, smer rotacije i polarnu orijentaciju, ovaj metod je bio važan korak ka modeliranju oblika asteroida, a u kombinaciji sa drugim metodima, bitno je doprineo stvaranju modernih metoda za modeliranje.
Postulati ovog metoda su:
- na krivoj sjaja postoji tačka koja ima konstantnu fazu i može se detektovati na svim posmatranim krivama (u praksi se za ovu tačku gotovo uvek uzima maksimum)
- ne postoji precesija pri kretanju asteroida
Obe navedene aproksimacije ne predstavljaju problem; druga je zadovoljena za sve osim pojedinih, retkih asteroida (često kontaktnih dvojnih, koji su i inače van domašaja klasičnih metoda), a prva se svodi na odsustvo globalnih nekonveksnosti oblika, što ne važi jedino za veoma male asteroide (manje od 10 km, npr. Kaulla, 1996).
Osnovna jednačina ovog metoda je tzv. jednačina fotometrijske astrometrije, koja daje zavisnost sideričkog perioda od geometrije posmatranja i epoha maksimuma:
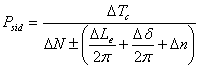 (17)
(17)
Pri tome je ![]() - vremenski interval između dve epohe (tj. dva
pojavljivanja maksimuma),
- vremenski interval između dve epohe (tj. dva
pojavljivanja maksimuma), ![]() - ceo broj rotacija između tih pojavljivanja,
- ceo broj rotacija između tih pojavljivanja, ![]() - razlika longituda tačke asteroida na pravcu centar
asteroida-Zemlja prve i druge krive,
- razlika longituda tačke asteroida na pravcu centar
asteroida-Zemlja prve i druge krive, ![]() - razlika ugla između pravaca asteroid-Zemlja i
asteroid-Sunce, kod prve i druge krive, a
- razlika ugla između pravaca asteroid-Zemlja i
asteroid-Sunce, kod prve i druge krive, a ![]() - popravka za broj rotacija
- popravka za broj rotacija ![]() , koja je jednaka celom delu broja revolucija u intervalu
, koja je jednaka celom delu broja revolucija u intervalu ![]() . Znak plus označava progradnu, a znak minus retrogradnu
rotaciju. Veličine
. Znak plus označava progradnu, a znak minus retrogradnu
rotaciju. Veličine ![]() i
i ![]() se mogu povezati sa koordinatama pola, pa se dobija
jednačina sa sideričkim periodom i ekliptičkim koordinatama pola
se mogu povezati sa koordinatama pola, pa se dobija
jednačina sa sideričkim periodom i ekliptičkim koordinatama pola
![]() i
i ![]() kao nepoznatim veličinama. Svaka kriva daje jednu
jednačinu, a sve jednačine se rešavaju prvo sa znakom plus, a zatim sa
znakom minus u imeniocu. U
praksi se pokazalo da je za rešavanje ovakvog sistema
potrebno 6-10 krivih sjaja iz jedne opozicije, i još nekoliko krivih iz
drugih opozicija. Naravno, ovako veliki posmatrački materijal obično nije
dostupan, pa je ova varijanta fotometrijske astrometrije danas napuštena.
kao nepoznatim veličinama. Svaka kriva daje jednu
jednačinu, a sve jednačine se rešavaju prvo sa znakom plus, a zatim sa
znakom minus u imeniocu. U
praksi se pokazalo da je za rešavanje ovakvog sistema
potrebno 6-10 krivih sjaja iz jedne opozicije, i još nekoliko krivih iz
drugih opozicija. Naravno, ovako veliki posmatrački materijal obično nije
dostupan, pa je ova varijanta fotometrijske astrometrije danas napuštena.
Bolji postupak dao je Mihalovski
(Michalowski, 1988). Osnovna ideja ovog postupka je uvođenje, umesto
popravki ![]() i
i ![]() , tzv. bisektrise faznog ugla, čija longituda
, tzv. bisektrise faznog ugla, čija longituda
![]() figuriše u ovoj varijanti jednačine fotometrijske
astrometrije:
figuriše u ovoj varijanti jednačine fotometrijske
astrometrije:
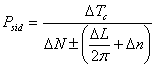 (18)
(18)
Popravka je povezana sa polarnom orijentacijom sledećim obrascem:
![]() (19)
(19)
Vektor
![]() se dobija iz relacija:
se dobija iz relacija:
![]() (20)
(20)
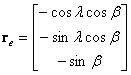 (21)
(21)
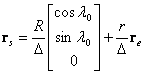 (22)
(22)
Pri tome su
![]() ,
, ![]() - koordinate asteroida na nebu, a
- koordinate asteroida na nebu, a
![]() ,
, ![]() ,
,![]() - redom rastojanja Sunce-asteroid, Zemlja-asteroid,
Zemlja-Sunce. Smisao i izvođenje ovih obrazaca dat je u Dodatku 1.
- redom rastojanja Sunce-asteroid, Zemlja-asteroid,
Zemlja-Sunce. Smisao i izvođenje ovih obrazaca dat je u Dodatku 1.
Rešavanje sistema jednačina (18)
vrši se, kao i u prethodnoj varijanti, sa plus i sa minus znakom. Takođe se
postavlja problem određivanja kvadranta ugla
![]() iz jednačine (19), ali se u praksi jasno vidi koji
slučajevi imaju rešenja, a koji ne. Za dobijanje rešenja, dovoljno je imati
šest krivih sjaja iz različitih opozicija.
iz jednačine (19), ali se u praksi jasno vidi koji
slučajevi imaju rešenja, a koji ne. Za dobijanje rešenja, dovoljno je imati
šest krivih sjaja iz različitih opozicija.
Iz ovih izlaganja je jasno da je glavna prednost metoda epohe mali broj početnih pretpostavki, kao i jednostavnost računa. Međutim, razvojem metoda amplitude-magnitude, kao i metoda koji omogućavaju modeliranje površine, metodi epohe su uglavnom pali u zaborav, između ostalog i zbog velikog posmatračkog materijala koji zahtevaju. Tek u kombinovanim metodima, pomenutim u petom odeljku, ovaj metod je postao zanimljiv i za modernu astronomiju; u ovim metodima, metod epohe se često i ne oslanja na tradicionalnu fotometrijsku astrometriju.
|
Sadržaj | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | sledeća strana |
