Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5

Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA

---

Dodatak 5 – Inverzija integralne jednačine
Fredholmovog tipa prve vrste

Kao što je napomenuto u sedmom odeljku, rešavanje dobijene integralne jednačine (39) zasniva se na minimizovanju odstupanja od tačnog rešenja i obezbeđivanju stabilnosti rešenja. Jasno je da je broj mogućih rešenja beskonačan, i da je moguće dobiti rešenje koje će proizvoljno dobro opisivati posmatranja, ali će samo uzak interval rešenja imati smisla, tj. omogućiće rekonstrukciju oblika. Kod inverzije krivih sjaja javlja se još i zahtev za konveksnošću rešenja, koji mora biti zadovoljen da bi formalizam izložen u šestom i sedmom odeljku bio korektan.

Procedura koja omogućava dobijanje rešenja na opisani način može se izgraditi na formalizmu Bajesove teorije. Jednačina (39) spada u tzv. Fredholmove jednačine prve vrste. U konciznom obliku ona se može zapisati kao:

    (D5.1)

Leva strana (koja odgovara poznatoj veličini koja se, po tradiciji, u algebarskim i diferencijalnim jednačinama, piše sa desne strane) označava posmatranja, tj. krive sjaja, dok integral sa desne strane sadrži tzv. jezgro (koje odgovara zakonu odbijanja, ili, uopšte, nekom “instrumentu” ili procesu koji “transformiše” nepoznatu veličinu u “vidljivi oblik”) i nepoznatu veličinu – oblik. Sa  je označena greška merenja (koja se mora uzeti u razmatranje pri samom procesu rešavanja). Neka je sa  označeno rešenje u diskretnom obliku, tj. u obliku matrice Laplasovih koeficijenata, sa  jezgro u matričnom obliku, sa matrica koja sadrži Laplasove koeficijente krivih sjaja, čije su greške date u obliku matrice kovarijacije , koja sadrži grešku sadržanu u . Bajesova teorema daje:

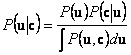    (D5.2)

Imenilac predstavlja konstantu, čija vrednost nije bitna. Za verovatnoću  može se uzeti Gausova raspodela, sa centrom  i matricom kovarijacije :

    (D5.3)

Za centar navedene raspodele može se uzeti sfera ili elipsoid, dok matrica kovarijacije, koja predstavlja dozvoljena odstupanjaod početnog, pravilnog oblika. Izbor ove matrice nije jednostavan zadatak: ona mora da dozvoljava modeliranje dovoljno nepravilnih oblika, ali da zadrži konveksnost i onemogući dobijanje rešenja koja nisu “glatka” ili pokazuju velike promene sa malim varijacijama početnih podataka.

Za uslovnu verovatnoću  se takođe može usvojiti Gausova raspodela:

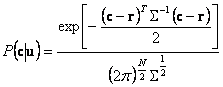    (D5.4)

Zamenom jendačina (D5.3) i (D5.4) u (D5.2) dobija se izraz za uslovnu verovatnoću . Maksimalizacijom ovog izraza dobija se rešenje , koje, formalno posmatrano, maksimalizuje i a posteriori verovatnoću traženog rešenja, tj. minimalizuje odstupanja od posmatranja, i a priori verovatnoću nađenog rešenja, koja je određena matricom kovarijacije i centrom raspodele (D5.3), koja sadrži zahteve za stabilnošću rešenja i konveksnošću oblika. Maksimizacija se može uraditi korišćenjem pogodne iterativne procedure, uz stalnu kontrolu toka proračuna, jer i u ovoj fazi može doći do nestabilnosti ili “upadanja” u singularnosti, naročito ako matrica kovarijacije  nije pogodno odabrana.

vrh