Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5

Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA

---

2. Fizičke teorije odbijanja
svetlosti sa površine asteroida

Prvi radovi na polju odbijanja svetlosti sa površine asteroida i, uopšte, sa površine planeta, datiraju još iz druge polovine devetnaestog veka. Prva razmatranja, zapravo, nisu ni uključivala nikakvu fizičku teoriju odbijanja, već su se zasnivala na nekim intuitivnim pretpostavkama i geometrijskim aproksimacijama. U ovom periodu data su dva zakona odbijanja, Lambertov i Lomel-Zeligerov. Lambertov zakon je dat izrazom:

    (1)

Element površine i svetlost koju on odbije označeni su sa  i , redom. Sa  je označen sferni albedo (odnos primljene i odbijene svetlosti u svim pravcima), a sa  i - redom odbojni i upadni ugao. Ovaj zakon sledi neposredno iz osnovnih zakona optike i definicije sfernog albeda, a važi za glatku, jednobojnu, homogeno osvetljenu sferu. Istorijski značaj ovog zakona je u tome što je omogućio da se daju kvantitativne procene sjaja asteroida u ranoj fazi njihovog proučavanja; danas je, naravno, napušten.

Lomel-Zeligerov (Lommel-Seeliger) zakon je postavljen 1877. godine, i predstavlja daleko razumniju aproksimaciju nego Lambertov. On se odnosi na proizvoljno glatko telo, osvetljeno tačkastim izvorom svetlosti. Osvetljenost elementa površine data je izrazom:

    (2)

Konstanta  je povezana sa geometrijskim albedom (odnos udela odbijene svetlosti posmatranog tela i udela svetlosti koju odbije beli disk na jediničnom rastojanju od Sunca) i još nekim karakteristikama površine; u većini slučajeva tačna vrednost osvetljenosti nije značajna, pa se konstanta zanemaruje ili se uzima proizvoljna, iz numeričkih razloga pogodna, vrednost. Važna osobina ovog zakona je da se za opoziciona posmatranja () dobija tzv. geometrijsko odbijanje svetlosti, pri kome je ukupna osvetljenost asteroida proporcionalna projekciji poprečnog preseka (što je našlo važnu primenu kod metoda amplitude-magnitude). Inače, ovakav oblik Lomel-  Zeligerovog zakona, nešto opštiji od prvobitnog Lomelovog i Zeligerovog pristupa, u literaturi se naziva i Hapke-Irvinov zakon.

Mada su se još početkom osamdesetih godina pojavili mnogo bolji zakoni, zasnovani na fizičkim teorijama odbijanja svetlosti, Lomel-Zeligerov zakon je sve do danas ostao aktuelan, pre svega zbog svoje jednostavnosti i pogodnosti kod nekih komplikovanih numeričkih proračuna. Ipak, treba imati na umu inferiornost ovog zakona u odnosu na novije zakone, i koristiti ga samo onda kada mala tačnost korišćenog metoda modeliranja obesmišljava korišćenje preciznijih zakona, ili proračuni postaju previše komplikovani u slučaju korišćenja nekog drugog zakona.

Fizička teorija koja je do sada najbolje opisala sve važne efekte pri odbijanju svetlosti sa površine planeta, i koja je dovoljno opšta da objasni odbijanje svetlosti kako sa površine asteroida tako i sa površine planeta i satelita, je teorija koju su 1981. godine dali Lume i Bauel (Lumme, Bowell, 1981a, b). Ova teorija uspeva da objasni kako same krive sjaja asteroida, tako i njihove fazne krive (zavisnost magnitude redukovane na jedinično rastojanje od Zemlje i Sunca od faznog ugla). Osnovni cilj ovog članka ne dozvoljava detaljniji opis ove teorije; ipak će biti date osnovne karakteristike i najvažnije primene ove teorije, zbog njihovog značaja pri modeliranju asteroida.

Lume-Bauelova teorija je pretendovala da, pre svega, objasni fazne krive. Naime, iz posmatračkih podataka može se zaključiti da redukovana magnituda uglavnom linearno opada sa povećanjem faznog ugla, osim za fazne uglove manje od  (vrednost ovog praga varira kod različitih asteroida), kada je redukovana magnituda veća nego što to predviđa linearna zavisnost. Ova pojava poznata je kao opozicioni efekat ili, u starijoj literaturi, kao opozicioni skok (engl. opposition spike).

Lume-Bauelova teorija tretira površinu planete kao sloj čestica slučajnog, nepravilnog oblika, određene gustine “pakovanja”, tj. koje zauzimaju određeni deo ukupne zapremine površine (u daljem tekstu – zapreminska gustina, engl. volume density). Na površini postoje udubljenja (engl. holes). Globalne optičke karakteristike površine određuju se statističko-probabilističkim postupkom, a u obzir se uzimaju pojedinačno i višestruko odbijanje (engl. single scattering, multiple scattering), kao i uticaj senki (engl. shadowing), zapreminske gustine i krševitost površine (engl. surface roughness).Detalji vezani za fizički smisao izraza za osvetljenost elementa površine su komplikovani i ne mogu biti razmatrani, a mogu sa naći u originalnom radu Lumea i Bauela (Lumme, Bowell, 1981a). Osvetljenost elementa površine ovde zavisi i od faznog ugla .

Optičke karakteristike površine opisuje pet parametara: albedo jednostrukog odbijanja  (engl. single scattering albedo), faktor asimetrije  (engl. assymetry factor), zapreminska gustina , udeo površine pokriven šupljinama  i krševitost . Osvetljenost elementa površine je data sa:

    (3)

Parametar  odgovara jednostrukom odbijanju i iznosi:

    (4)

pri čemu parametri sa desne strane označavaju, redom, Henji-Grinštajnovu (Henyey-Greenstein) faznu funkciju, funkciju koja opisuje efekte senki i funkcija koja odgovara efektima krševitosti, koje iznose:

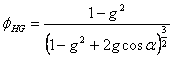    (5)

    (6)

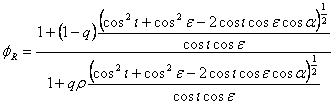    (7)

Funkcija  opisuje višestruko odbijanje i može se aproksimirati sa:

    (8)

Sa  je označena generalizacija Čandrasekarove (Chandrasekhar, 1950) funkcije, koja ima oblik:

    (9)

pri čemu je:

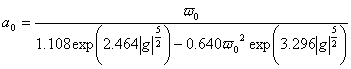    (10)

    (11)

Naročito su važni izrazi za izrazi za integralni sjaj, kojima se mogu objasniti fazne krive, a koji je, u vidu tzv. H-G sistema, usvojen kao standardni sistem za izražavanje sjaja asteroida. Normirani integralni sjaj pri faznom uglu , u formalizmu Lume-Bauelove teorije tradicionalno obeležen sa , predstavljen kao kombinacija jednostruko i višestruko odbijene svetlosti, iznosi (navedeni izraz poznat je kao Lume-Bauelov zakon):

      (12)

Parametri ,  su veličine koje zavise od faznog ugla i odgovaraju, redom, integralnom sjaju u slučaju jednostrukog i višestrukog odbijanja, dok je  tzv. parametar nagiba (slope parameter). To je težinski parametar između  i , delimično statističke prirode, koji se u praksi određuje iz posmatračkog materijala; uzima se da je konstantan je za dati asteroid (tačnost ove tvrdnje je diskutabilna, ali se za većinu praktičnih primena Lume-Bauelovog zakona može smatrati bar kao dobra aproksimacija). Ovaj parametar odgovara nagibu linearnog dela fazne krive. Najpouzdaniji izvor vrednosti za  je Lagerkvistov fotometrijski katalog asteroida (Lagerkvist et al, 1996).

Izrazi za  i  uključuju, ponovo, težinsko slaganje dva efekta: uticaj senki i uticaj neravnina površine: 

,      (13) 

,      (14)

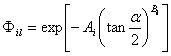,      (15)

Težinski parametar  zavisi samo od faznog ugla i računa se po obrascu:

    (16)

Parametri , ,  su bezdimenzione konstante i određene su teorijski, a koriguju se iz dugoročnih posmatranja. Trenutno prihvaćene vrednosti su (Lagerkvist, Magnusson, 1990):

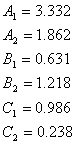
Na kraju, treba pomenuti i Hapkeov zakon (Happke), razvijen približno istovremeno sa Lume-Bauelovim (Happke, 1981), koji uvodi pet slobodnih parametara: albedo jednostrukog odbijanja , širina opozicionog talasa  (engl. opposition surge width), amplituda opozicionog talasa  (engl. opposotion surge amplitude), čestični fazni parametar  (engl. single-particle phase function parameter) i srednji nagib makroskopske krševitosti  (engl. average slope of macroscopic roughness). Ovaj zakon se takođe pokazao kao dobar, pa se često koristi pri modeliranju, ali po opštosti i primenljivosti na fazne krive zaostaje za Lume-Bauelovim zakonom.

vrh