Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5

Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA

---

Dodatak 3 – Integralni sjaj elipsoidnog modela

Kod metoda kao što je metod Kvaitkovskog neophodna je integracija sjaja asteroida u cilju dobijanja direktne zavisnosti amplitude od parametara modela.Integralni sjaj iznosi (up. (38)):

    (D3.1)

Oznake su identične kao u (38). Integracija se vrši u oblasti u kojoj su upadni i odbojni ugao veći od nule. Iz elementarne sferne trigonometrije slede veze ovih uglova sa asterocentričnim koordinatama i faznim uglom:

    (D3.2)

    (D3.3)

Iz navedenih jednačina lako se mogu dobiti oblasti u kojima su dati uglovi pozitivni, čime su određene granice integracije. Druga mogućnost je implementiranje kriterijuma vidljivosti u samu proceduru integracije, tj. zamena zakona odbijanja članom:

,  za     (D3.4)

, za     (D3.4)

Naravno, zavisnost  od preostale dve koordinate mora biti poznata. Za elipsoid važi:

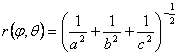    (D3.5)

Naravno, zbog simetrije, u ovom slučaju  je konstantno. Uvrštavanjem ovih rezultata i zakona odbijanja u (D3.1) daje traženi izraz za integralni sjaj. Integracija se može vršiti za celu krivu, ili samo za ekstreme (tj. nekoliko tačaka u blizini ekstrema), iz čega se može dobiti amplituda.

Naravno, ovaj postupak je moguć za bilo koji oblik, ali u praksi nema smisla ići dalje od relativno jednostavnih modela (npr. Jakobijevi elipsoidi, kombinacija elipsoida i sferne površi, itd). U tom slučaju, potrebno je iskoristiti opšti oblik izraza (D3.5), koji se može dobiti iz jednačine (36).

vrh