Sadržaj
Glava1
Glava 2
Glava 3
Glava 4
Glava 5
Glava 6
Glava 7
Glava 8
Glava 9
Dodatak 1
Dodatak 2
Dodatak 3
Dodatak 4
Dodatak 5

Mihailo Čubrović
MODELIRANJE OBLIKA I KARAKTERISTIKA POVRŠINE ASTEROIDA
KORIŠĆENJEM OPTIČKIH KRIVIH SJAJA

---

Dodatak 2 – Formalizam elipsoidnog modela
kod metoda amplituda-magnituda

Za naredna razmatranja biće uvedena su dva pravougla koordinatna sistema. Prvi sistem  je orijentisan tako da ima - osu u pravcu asteroid-posmatrač, a - osa je orijentisana tako da - ravan sadrži pravac asteroid-Sunce. Ose drugog sistema  su orijentasane u pravcu poluosa asteroida , , . Centri oba sistema se poklapaju sa centrom asteroida. Na slici 5 prikazani su pomenuti koordinatni sistemi i važni uglovi. Uglovi  i  nisu značajni, i koriste se jedino kod nekih pomoćnih transformacija.

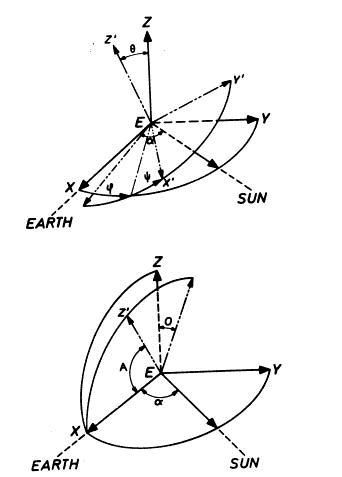
Slika 5- Koordinatni sistemi korišćeni u ovom odeljlu. Preuzeto iz: Surdej, Surdej, 1978.

Figure 5- Coordinate systems used in this section. Taken from: Surdej, Surdej, 1978.

Matrica transformacije prvog sistema u drugi data je sa:

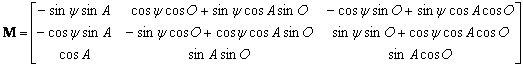    (D2.1)

Površina projekcije asteroida može se naći kao površina preseka asteroida i valjka čija je generatrisa paralelna pravcu Zemlja-asteroid, koja iznosi (Barucci, Fulchignoni, 1982):

    (D2.2)

gde je  matrica koja karakteriše međusobni položaj valjka i asteroida, i može se izraziti preko matrice transformacije:

,      (D2.3)

gde je , redom. Zamenom odgovarajućeg elementa matrice  iz (D2.3) u (D2.2) dobija sa izraz za površinu projekcije (24).

Pri proizvoljnoj geometriji posmatranja, projekcija osvetljenog dela asteroida je jednaka:

    (D2.4)

gde je - površina projekcije asteroida na ravan normalnu na pravac Sunce-asteroid. Ova površina se računa slično kao i u prethodnom slučaju, i iznosi:

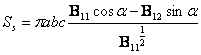    (D2.5)

Matrica  iznosi:

    (D2.6)

pri čemu je - matrica  transformisana u koordinatni sistem dobijen rotacijom sistema  tako da - osa ima pravac asteroid-Sunce:

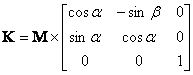    (D2.7)

Zamenom (D2.6-7)  u (D2.5) i razvojem u Tejlorov red u okolini nule, uz zanemarivanje članova višeg reda se dobija:

    (D2.7)

odakle, zamenom u (D2.4), sledi jendačina (32). Funkcija  ima sledeći oblik (radi konciznosti je izostavljeno pisanje zavisnosti od ):

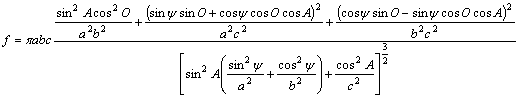    (D2.8)

Jednačina (32), koja daje traženu površinu, zbog složenosti funkcije , nema nikakvu praktičnu primenu; njen značaj je pre svega teorijski: ona pokazuje da pri malim faznim uglovima (zbog kvadrata faznog ugla koji u njoj figuriše) opoziciona aproksimacija (24) sasvim dobro opisuje realnu situaciju.

vrh